সেগমেন্ট ট্রি (Segment tree) একটি গুরুত্বপূর্ণ ডাটা স্ট্রাকচার। এই ডাটা স্ট্রাকচার টি বিভিন্ন অ্যালগরিদম এ রেঞ্জ অপারেশন চালাতে ব্যবহার করা হয়। আপনারা এমন কিছু প্রবলেম দেখে থাকতে পারেন যেখানে, একটা Array দেয়া থাকে N সাইজ এর আর বলা হয় ঐ Array টার উপর Q টি Operation চালাতে হবে। প্রত্যেকবার ঐ Array এর i তম index এর মান একটা ভ্যালু V দিয়ে আপডেট করতে হবে পরে ঐ Array এর একটা রেন্জ l থেকে r এর যোগফল/মিনিমাম/ম্যাক্সিমাম প্রিন্ট করতে হবে।
সলুশন ১:
প্রতিবার Query করার সময় আমরা ঐ Array এর i তম index V দ্বারা Update করবো। পরে l থেকে r পর্যন্ত যোগফল/মিনিমাম/ম্যাক্সিমাম বের করে প্রিন্ট করবো। সহজ হিসাব।
আসলে ঝামেলাটা তখনই হয় যখন ঐ প্রবলেমে নির্দিষ্ট সময় দেয়া থাকে। ধরা যাক সময়টা ২ সেকেন্ড। তো এখন যা হবে তা হলো N<=10^5,Q<=10^5 হলে সলুশন ১ ২ সেকেন্ড এ Answer প্রিন্ট করতে পারবে না। তাই সবশেষে দেখা যাবে আপনার সলুশন TLE খেয়ে বসে আছে। কারন তখন আপনার ঐ ইনডেক্স i এ আপডেট করার টাইম কমপ্লেক্সিটি হবে O(1) কিন্তু l থেকে r রেন্জের SUM/MIN/MAX প্রিন্ট করার কমিপ্লেক্সিটি হবে O(N)। Q টা Query থাকে মোট কমপ্লেক্সিটি O(N*Q)। এখানেই ঘটে বিপত্তি। N*Q = 10^10!
সলুশন ২:
এই প্রবলেমটা সেগমেন্ট ট্রি (Segment Tree) নামক ডাটা স্ট্রেকচার ব্যবহার করে খুব সহজেই সমধান করা যায়। শুধু এ ধরনের না, আরও অনেক প্রবলেম আছে যা সেগমেন্ট ট্রি ব্যবহার করে সমাধান সম্ভব। সেগমেন্ট ট্রিতে, আপডেট ও কুয়েরি উভয়েরই কমপ্লেক্সিটি O(logN) [ 2 base log]। কিন্তু বিল্ড (build) কমপ্লেক্সিটি O(N)।

সেগমেন্ট ট্রি বিল্ড(Build)/তৈরি করা:

N=8 এর জন্য একটা সেগমেন্ট ট্রি এর নকশা উপরের চিত্রে দেখানে হয়েছে। ধুসর গুলোকে আপাতত বাদ দেই। আমাদের কাছে মোট ৮ টি জায়গা আছে।
আমরা এখানে রেফারেন্স Array হিসেবে arr[8] = {1,2,3,4,5,6,7,8} ব্যবহার করবো। N=8, L=0,R=7
Note: এখানে সেগমেন্ট ট্রি এর Tree অ্যারে তে আমরা ১ থেকে ইন্ডেক্সিং করবো এবং মূল অ্যারে তে 0 থেকে করবো, এবং রিকার্শন সম্পর্কে ধারনা ধাকতে হবে। মার্জ শর্ট জানলে বুঝা সহজ হয়ে যাবে।
আমরা যা করবো তা হলো এই জায়গাগুলোকে আমরা প্রথমে ২ ভাগে ভাগ করবো: [1-4] এবং [5-8]। যদি আমাদের কাছে [L,R] দুইটি সীমা থাকে তবে একে দুইভাগ করলে দাড়াবে [L,mid] এবং [mid+1,R]। এখানে mid = (L+R)/2 [ইন্টিজার ডিভিশন]।
এভাবে আমরা আমাদের সীমাকে ততক্ষন পর্যন্ত ভাঙতে থাকবো যতক্ষন না পর্যন্ত আমাদের সেগমেন্টে একটিমাত্র সংখা থাকে অর্থাৎ L=R হয়।
এটা ভাবার কোন কারন নাই যে N, ২ এর ঘাত হলেই এটা সম্ভব। বরং N=3 যদি হয় তবে
| 1 2 3 4 | [0,2] হলে mid = (0+2)/2=1 তখন, দুটি ভাগ [0,1],[2,2] এখানে শেষের [2,2] এর জন্য L=R কিন্তু প্রথমটাতে কাজ করতে হবে। L=0,R=1 এর জন্য mid=1, সুতরাং [0,1]=[0,0],[1,1]। |
এখন কথা হলো আমরা তো চিত্রের মাধ্যমে সুন্দর করে বুঝে ফেলতে পারি কিন্তু, এটাকে কোডে করবো কিভাবে? এবার ছবি ২ এ তাকান। উপরের ধুসর সংখ্যাগুলো খেয়াল করেন। এখানে প্রতিটা সেগমেন্টের একটি করে নাম্বার দেয়া হয়েছে। এদের একটা বিশেষত্ব আছে। একটা বিষয় দেখেন, যেকোন সংখ্যা x এর বামে সবসময় 2x এবং ডানে সবসময় 2x+1 থাকে। আবার তার প্যারেন্ট হয় x/2. এই টেকনিক ব্যবহার করে খুব সহজেই সেগমেন্ট ট্রি বানানো যাবে।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | void build(int L,int R,int at){ if(L==R){ tree[at]=arr[L]; return; } int mid = (L+R)/2; int leftNode = at*2; int rightNode = at*2+1; build(L,mid,leftNode); build(mid+1,R,rightNode); tree[at] = tree[leftNode]+tree[rightNode]; } //Call it using build(0,Size of the array -1 ,1); |
tree[] অ্যারেতে আমরা ট্রি টাকে স্টোর করবো। ট্রি অ্যারের সাইজ হবে ইনপুট অ্যারের 4 গুণ। build ফাংশনটি arr অ্যারে থেকে ট্রি তৈরি করে দিবে। build এর প্যারামিটার হলো L,R,at এখানে at=বর্তমানে কোন নোডে আছি এবং L,R হলো বর্তমানে কোন রেঞ্জে আছি। শুরুতে আমরা নোড ১ এ থাকবো এবং 0-sizeOfarray-1 রেঞ্জে থাকবো(ট্রি এর ছবিটা দেখেন)।
যদি (L==R) হয়ে যায় তাহলে আমরা শেষ নোডে পৌছে গেছি, এখানে যোগফল হবে অ্যারেতে যে ভ্যালু আছে সেটাই, সেটাকে ট্রিতে স্টোর করে রিটার্ণ করে দিলাম। যদি (L==R) না হয় তাহলে অ্যারেটা কে দুই ভাগে ভাগ করতে পারি। বাম পাশের নোডের ইনডেক্স হবে at*2 এবং ডান পাশেরটা at*2+1। এবং অ্যারেটাকে ভাঙবো ঠিক মাঝখানে। এবার রিকার্সিভলি দুই পাশে build কল করলে বাম এবং ডান পাশের ছোটো অংশের যোগফল বের হয়ে যাবে। দুইপাশের কাজ শেষ হয়ে গেলে বর্তমান নোডের যোগফল হবে বাম এবং ডানের নোডের যোগফল।
বুঝতে সমস্যা হলে ট্রি টি খাতায় সিমুলেট করলেই সব পরিষ্কার হয়ে যাবে।
PS: যদি বলা থাকে কোন সেগমেন্ট এ কত সংখ্যা আছে তবে আমরা একদম শেষ সেগমেন্টে গিয়ে সঠিক সংখ্যা বসাবো এবং ফিরে এসে সঠিক sum/min/max রাখবো। এই টিউটোরিয়ালে আমি যোগফল এরটা দেখাবো
| 1 | tree[at] = tree[leftNode]+tree[rightNode]; |
খেয়াল করলে দেখা যায় যে, আমাদের প্রথম লেভেলে সেগমেন্ট ১ টি, ২য় লেভেলে ২ টি, এর পরে ৪ টি এভাবে ৮,১৬,৩২,N আকারে বাড়তে থাকে। যা যোগ করলে দঁাড়ায় 2N. সুতরাং আমাদের বিল্ড এর কমপ্লেক্সিটি O(n).
এইবার আমাদের কুয়েরি কারার একটা ফাংশন দরকার যেটা যেকোন রেন্জ l-r এর যোগফল বের করে দিতে পারবে।
সেগমেন্ট ট্রিতে কুয়েরি করা:
ধরেন আমরা যেকোন রেন্জ l=0, r=5 (0 index) এর যোগফল চাই। নিচের চিত্রটা দেখি।
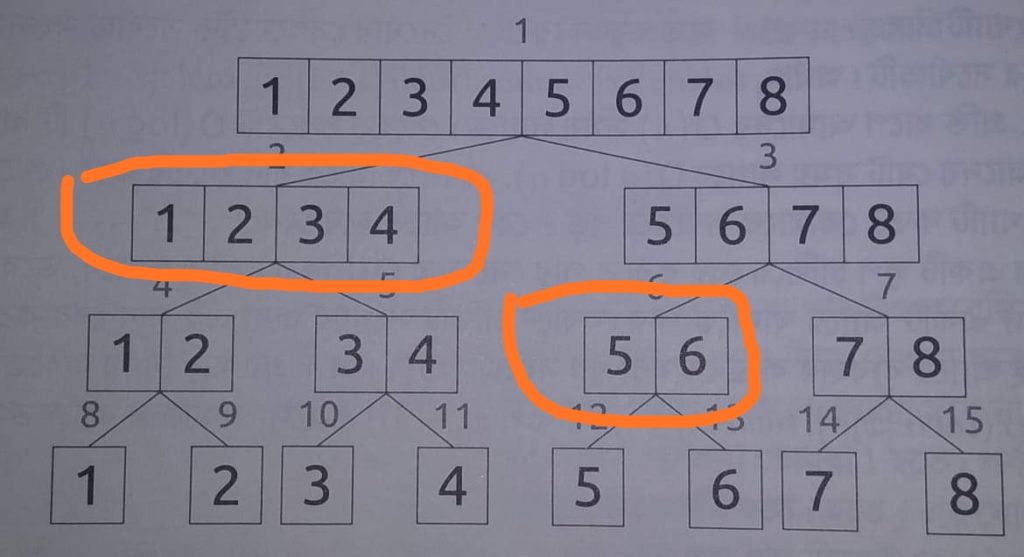
আমাদের কুয়েরি ফাংশনের কাজ হবে শুধু রিলেভেন্ট নোডগুলোর যোগফল বের করা। কোডটা build ফাংশনের মতোই হবে তবে কিছু কন্ডিশন অ্যাড করতে হবে। ধরেন আপনি এমন একটা নোডে আছো যেখানে bL-eR রেঞ্জের যোগফল আছে। আপনি এই নোডটা রিলেভেন্ট কিনা সেটা কিভাবে বুঝবে? এখানে ৩ ধরণের ঘটনা ঘটতে পারে:
- r<bL || eR<l, এখানে সেগমেন্টা পুরোপুরি বাইরের। নেয়ার দরকার নেই। ০ রিটার্ন করে দিবো।
- l<=bL&&r>=eR। সেগমেন্টটা রিলেভেন্ট। এই নোডের ভ্যালু রিটার্ন দিবো।
- দুইটার একটাও না, মানে আংশিক
3 নং কেসের জন্য আমরা সেগমেন্ট টাকে আরও ভেঙে রিলেভেন্ট অংশটুকু নিবো।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | int query(int l,int r,int L,int R,int at){ //Here L and R is bL and eR mentioned above. if(l>R||r<L) return 0; if(l<=L&&R<=r){ //if segment matches the range we need return tree[at]; } int mid=(L+R)/2; int leftNode = at*2; int rightNode = at*2+1; int s1 = query(l,r,L,mid,leftNode); //Visiting left int s2 = query(l,r,mid+1,R,rightNode); //Visiting right return s1+s2; //return s1+s2 after Visiting } |
ট্রিতে কুয়েরি করার কমপ্লেক্সিটি O(log n) প্রতিবার কুয়েরির শেষ লাইনে আমরা দুইটা নোড থেকে প্রাপ্ত আউটপুট কলার ফাংশনকে দিয়েছি।
সেগমেন্ট ট্রি (Segment tree) ট্রি তে Update আপডেট করা:
ট্রি আপডেট করা আর বিল্ড করার কোড প্রায় একই। শুধু এখানে একটা শর্ত দিয়ে দেয়া আছে। শর্তটা হলো আমাদের array তে যে পজিশন এ আপডেট করবো, যদি mid এর মান তার থেকে বেশি হয় তবে আমরা leftNode এ ভিজিট করবো, না হলে rightNode এ ভিজিট করবো (বিল্ড করার সময় দুইটাতেই করতাম)। আপডেট করা শেষ হলে আমরা নতুন ভ্যালু দিয়ে tree এর parent node গুলো আপডেট করে দিবো। এখানে টাইম কমপ্লেক্সিটি O(log n) । Done! আপডেট ফংশন
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | void update(int value,int index,int L,int R,int at){ if(L==R){ tree[at]=value; return; } int mid = (L+R)/2; int leftNode = at*2; int rightNode = at*2+1; if(index<=mid)//go left update(value,index,L,mid,leftNode); else //go right update(value,index,mid+1,R,rightNode); tree[at] = tree[leftNode]+tree[rightNode]; } //Call it using update(value,index of the array,0,ArraySize-1,1) |
সব মিলিয়ে সেগমেন্ট ট্রি (Segment tree) কোডটা দাড়ায় নিম্নরুপ:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 | /* Sharif Hasan - CSE, PUST Mar 31, 2020 04: 59 PM */ #include<bits/stdc++.h> using namespace std; int tree[4*(7+1)]; int arr[8]; void build(int L,int R,int at){ if(L==R){ tree[at]=arr[L]; return; } int mid = (L+R)/2; int leftNode = at*2; int rightNode = at*2+1; build(L,mid,leftNode); build(mid+1,R,rightNode); tree[at] = tree[leftNode]+tree[rightNode]; } void update(int value,int index,int l,int r,int at){ if(l==r){ tree[at]=value; return; } int mid = (l+r)/2; int leftNode = at*2; int rightNode = at*2+1; if(index<=mid) update(value,index,l,mid,leftNode); else update(value,index,mid+1,r,rightNode); tree[at] = tree[leftNode]+tree[rightNode]; } int query(int l,int r,int L,int R,int at){ if(l>R||r<L) return 0; if(l<=L&&R<=r){ //if segment matches the range we need return tree[at]; } int mid=(L+R)/2; int leftNode = at*2; int rightNode = at*2+1; int s1 = query(l,r,L,mid,leftNode); //Visiting left int s2 = query(l,r,mid+1,R,rightNode); //Visiting right return s1+s2; //return s1+s2 after Visiting } /*Main function*/ int main() { cout<<"Enter eight number:\n"; int i; for(i=0;i<8;i++){ cin>>arr[i]; } build(0/*start index*/,7/*end index*/,1/*begining node of the tree*/); int l,r; cout<<"Enter ranger l to r to query 0<=l<=r<=<=7 (0 based index):\n"; cin>>l>>r; cout<<query(l,r,0,7,1)<<endl; cout<<"Enter a value and index to update at index:\n"; int index,value; cin>>value>>index; update(value,index,0,7,1); cout<<"Enter ranger l to r to query 0<=l<=r<=<=7 (0 based index):\n"; cin>>l>>r; cout<<query(l,r,0,7,1)<<endl; return 0; |
আমাদের কিছু বিষয় জেনে রাখতে হবে। প্রথমটা হলো মেমোরি কমপ্লেক্সিটি। ভূল দৈর্ঘের Array নিলে রানটাইম এরর খেয়ে যাবেন। তাই অ্যারে সাইজ এর ৪ গুন বেশি Array Tree হিসেবে নেওয়াই ভালো। এখানে আরও অনেক লেখা আছে। আবার যদি বলে update এর সময় আমরা array একটা তে আপডেট না করে m সংখ্যক করবো। তখন আবার আমাদের প্রতিটা index এর যেতে হবে। তখন এভাবে হবে না। TLE খেয়ে যেতে পারে। এর জন্য Lazy Propagation নামের একটা টেকনিক ব্যবহার করতে হয়। যা আমরা পরে জানবো। ঠিক মার্জ সর্টের মতো সেগমেন্ট্রি ট্রিও “ডিভাইড এন্ড কনকোয়ার” পদ্ধতিতে কাজ করে।
প্রোগ্রামিং: সেগমেন্ট ট্রি ডাটা স্ট্রাকচার। রেন্জ কুয়েরি: যোগফল
আজকের লেখাটা এ পর্যন্তই রাখতে চাই। লেখাটা বড় হওয়ায় ভূল হতে পারে। কারও কোন সমস্যা হলে কমেন্টে জানানোর অনুরোধ রইলো।



Vaiya, ai related akta problem link den.Amon problem j ta shudhu segment tree diyei solve kora possible onno kisu lagbe na!
https://toph.co/p/easy-prime
https://codeforces.com/contest/339/problem/D
https://codeforces.com/blog/entry/22616 ( এখানে অনেক গুলো আছে। ক্লাসিক গুলো সমাধান করেন )
query r operation bolta ashola ki bojai vai…ঐ Array টার উপর Q টি Operation চালাতে হবে।,,রতিবার Query করার সময় আমরা ঐ Array এর i তম
মানে হলো, যদি Q টি অপারেশন না করে ১ টি করা হয়, তখন কিন্তু আমরা লিনিয়ার O(N) সময়এই উত্তর দিতে পারবো। কিন্তু Q টি করা হলে O(Q*N) সময় সময় লাগবে। ধরেন Q=10^5 এবং N=10^5। সুতরাং Q*N = 10^10 টি হিসেব করতে হবে যদি আমরা প্রথম উপায়ে সমাধান করি