আমরা সেগমেন্ট ট্রি নিয়ে লিখায় দেখেছিলাম কিভাবে O(log n) টাইমে আমরা রেঞ্জ ম্যাক্সিমাম, মিনিমাম কুয়েরি করতে পারি। স্পার্স টেবিল (Sparse table) নিয়ে এই লিখায় দেখবো কিভাবে O(1) টাইমে রেঞ্জ মিনিমাম,ম্যাক্সিমাম বের করতে পারি। মিনিমাম এবং ম্যাক্সিমাম বের করার প্রসেস একই তাই আমরা মিনিমাম বের করার উপরে ফোকাস করবো। স্পার্স টেবিলের সাথে সেগমেন্ট ট্রি এর পার্থক্য হলো আমরা স্পার্স টেবিলে আপডেট করতে পারবো না কিন্তু সেগমেন্ট ট্রি তে আপডেট করা যাবে।
স্পার্স টেবিল (Sparse Table): সমস্যার বিবরণ
স্পার্স টেবিল (Sparse table) কেন ব্যবহার করবো তা বুঝার জন্য প্রথমে সমস্যাটি বুঝার চেষ্টা করবো। আমাদের একটি অ্যারে দেয়া আছে। আমাদেরকে যেকোনো রেঞ্জ থেকে এর মধ্যে মিনিমামবের করে দিতে হবে। আমরা খুব সহজেই O(n) সময়ে এর সমাধান করতে পারি। উদাহরণসরূপ নিচের কোডটি দেখি।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include<bits/stdc++.h> using namespace std; int main(){ int arr[]={2,35,4,51,6,7}; int Q; cin>>Q; while(Q--){ int l,r; cin>>l>>r; int mx=INT_MAX; for(int i=l;i<=r;i++){ mx=min(arr[i],mx); } cout<<mx<<endl; } } |
উপরের উদাহরণে আমাদের টি কুয়েরি করা হবে। প্রতিটি কুয়েরিতে রেঞ্জ ইনপুট দেয়া হবে। এখানে ১২ থেকে ১৪ নং লাইনে আমরা লুপের মাধ্যমে অ্যারেটির মিনিমাম বের করেছি।
এখন উপরের কোডের টাইম কমপ্লেক্সিটি । যা যথেষ্ট বড় ইনপুটের জন্য সময় বেশি নিবে। স্পার্স টেবিলের মাধ্যমে এই সমস্যার সমাধান তে করা সম্ভব। যেখানে প্রত্যেক কুয়েরি সময় নিবে।
Sparse Table Bangla tutorial/ Sparse Table Bengali tutorial
আমরা যেকোনো অ্যারেকে কিছু ২ এর সূচকীয় সংখ্যার যোগফল আকারে লিখতে পারি। যেমন । বা । এটা আমরা বুঝতে পারবো যদি এর বাইনারি উপস্থাপন খেয়াল করি। কে ডেসিমেলে রূপান্তর করার সময় ।
একই ভাবে আমরা যেকোনো রেঞ্জকে এমন কিছু রেঞ্জে ভাগ করে ফেলতে পারি। যেমন যদি এবং হয় তবে এর মধ্যে মোট ইলিমেন্ট আছে সাতটি। কে আমরা উপরের মত করে রূপে লিখতে পারি। তাই কে আমরা লিখতে পারি । এখানে সর্বোচ্চ টি সেগমেন্ট হতে পারে। যেখানে সেগমেন্ট সাইজ।
স্পার্স টেবিলের পেছনের মূল আইডিয়াটি হলো আমরা প্রথমে ২ এর সব সূচকীয় মানের (1,2,4,8,16,etc) দৈর্ঘ্যের জন্য যত সাব-অ্যারে আছে তার জন্য মিনিমাম প্রথমেই বের করে নিবো। যেমন নিচের চিত্রটি দেখি,
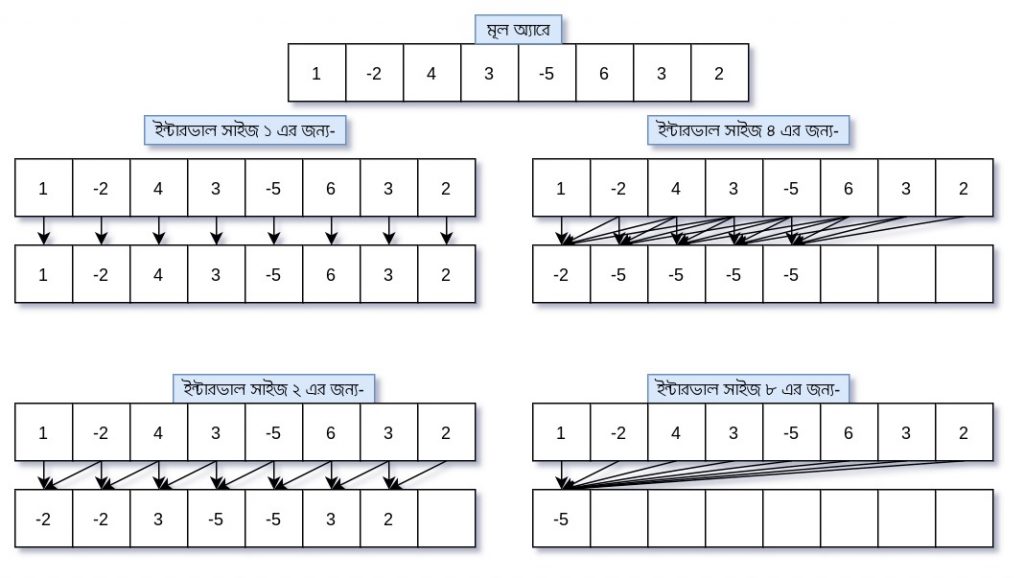
উপরের চিত্রে দৈর্ঘ্যের যত সাব অ্যারে আছে তার মিনিমাম বের করে নিয়েছি। আমরা দৈর্ঘ্যের কোন সাব অ্যারে নিইনি। কারণ 16, অ্যারের দৈর্ঘ্য 8 এর থেকে বড়। আমরা সাব অ্যারের মিনিমাম কিভাবে নিয়েছি আশা করি বুঝা যাচ্ছে। আরেকটু ব্যাখ্যা করি।
4 দৈর্ঘ্যের সাব অ্যারের মিনিমাম বের করাকে বিবেচনা করি। আমরা শুরু করেছি পর্যন্ত সাব অ্যারেকে নিয়ে []। এর মধ্যে মিনিমাম হচ্ছে -২। তাই আমরা অ্যারের 0 ইনডেক্স এ -2 রেখেছি। এরপর এর জন্যও বের করেছি। এক্ষেত্রে মিনিমাম -৫। একই ভাবে আমরা এগোতে থেকেছি যতক্ষণ না হয়।
এবার আমরা উপরের চিত্র গুলো একসাথে করে একটা 2D অ্যারের মত টেবিল তৈরি করি।
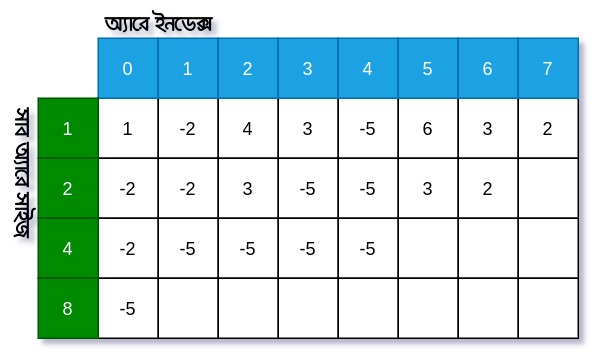
এখানে বাম থেকে ডানে আমরা অ্যারের ইনডেক্স নিয়েছি এবং উপর থেকে নিচে আমরা অ্যারের সাইজ অনুযায়ী মিনিমাম বের করে রেখেছি। এই টেবিলে একটি ফিল্ড আমাদের বলে দেয় যে, থেকে শুরু করে দৈর্ঘ্যের কোন সাব অ্যারের মিনিমাম কত। যেমন হলে আমরা বলতে পারি ইনডেক্স 1 থেকে শুরু করে 4 দৈর্ঘ্যের একটি সাব-অ্যারের মিনিমাম সংখ্যা হলো -5। এখন আমরা অ্যারের সাইজ গুলোকে রূপে লিখতে পারি এবং এর বদলে আমরা সূচক গুলকে ইনডেক্স হিসেবে ব্যবহার করতে পারি নিচের মত।
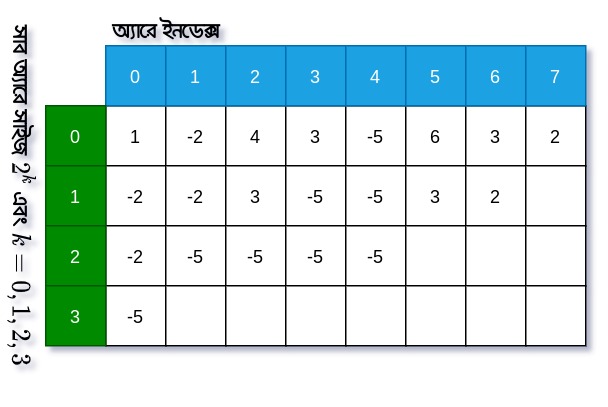
এখন এখানে যদি আমরা একটি ফিল্ড কে পরতে চাই তাহলে বলবো ইনডেক্স থেকে শুরু করে সাইজের কোন সাব অ্যারের মিনিমাম। এখানে এর সর্বোচ্চ মান হবে
স্পার্স টেবিল (Sparse table): লুক-আপ টেবিল প্রি-প্রসেসিং
আমদের একটি দ্রুততম রাস্তা বের করতে হবে অ্যারে হিসাব করে রাখার জন্য। শুরুতেই আমরা একটি 2D অ্যারে lookUpTable[Maxk+1][n] নিবো সাইজের। যেখানে । অর্থাৎ int lookUpTable[Maxk+1][n];।
আমরা সময়ে হিসাব করতে পারি। আমরা যা করবো প্রথমে থেকে পর্যন্ত লুপ চালাবো। তারপর আমরা থেকে যতক্ষণ না পর্যন্ত হয় ততক্ষণ পর্যন্ত লুপ চালাবো।
| 1 2 3 4 5 6 7 8 9 | int n=8; int arr[]={1,-2,4,3,-5,6,3,2}; int Maxk=__lg(n); int lookUpTable[Maxk+1][n]; for(int k=0;k<Maxk;k++){ for(int column=0;column+(1<<k)-1<n;column++){ // এখানে c থেকে 2^k পর্যন্ত সাব অ্যারের মিনিমাম বের করবো। } } |
আমরা ধরে নিই 2 (k=1) সাইজের সকল সাব-অ্যারের জন্য মিনিমাম আমরা বের করে নিয়েছি। এবার 4 সাইজের (k=2) সকল সাব অ্যারের মিনিমাম বের করার সময় আমরা 2 সাইজের সাব-অ্যারে গুলোকে কাজে লাগাতে পারি নাকি একটু দেখি। 4 সাইজের সাব অ্যারেকে আমরা 2 সাইজের 2 টি সাব অ্যারেতে ভেঙ্গে ফেলতে পারি।
যেমন হলে আমরা একে এবং এই দুই ভাগে ভাগ করতে পারি। যেহেতু আমরা আগেই 2 সাইজের সব সাব অ্যারের মিনিমাম হিসাব করেছিলাম তাই এই রেঞ্জের মিনিমাম হবে রেঞ্জের মিনিমাম এবং রেঞ্জের মিনিমাম এর মধ্যে ছোটটি।
আমরা প্রথমে 1 দৈর্ঘ্যের সব সাব অ্যারের মিনিমাম বের করে নিবো (ওই ইলিমেনটের মান)। তারপর আমরা 2 দৈর্ঘ্যের সাব অ্যারের মিনিমাম, তারপর 4 এভাবে এগোতে থাকবো।
কোডে যাবার আগে আমাদেরকে কয়কটি বিষয় নিয়ে পরিষ্কার ধারনা অর্জন করতে হবে।
lookUpTable[k][column] কে পড়বো কিভাবে?
lookUpTable[k][column] এর মানে হলো মূল অ্যারের ইনডেক্স থেকে সাইজের কোন সাব অ্যারের মিনিমাম এখানে জমা করা আছে।
সাইজের একটি অ্যারেকে কিভাবে দুইটি সাব-অ্যারেতে ভাঙতে পারি?
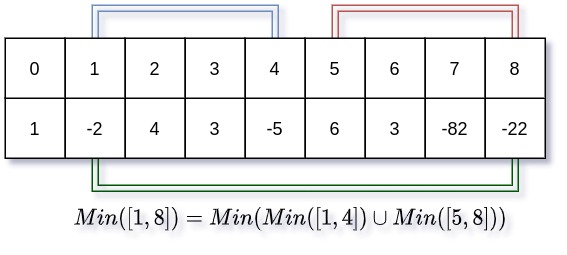
ধরা যাক মূল অ্যারের থেকে শুরু করে সাইজের একটি অ্যারেকে আমরা দুই ভাগে ভাগ করবো। আমরা দেখতে পাই এর অর্ধেক হলো বা । তাই আমরা প্রথম সেগমেন্ট নিবো 4 দৈর্ঘ্যের একটি সাব-অ্যারে যা থেকে শুরু হয়ে বা ইনডেক্স 4 এ শেষ। পরের সেগমেন্ট নিবো থেকে পর্যন্ত।
এখন lookUpTable[k][column] কে আমরা পরি column থেকে শুরু করে সাইজের কোন সাব অ্যারের মিনিমাম। উপরে ইনডেক্স 1 থেকে 4 পর্যন্ত আসলে একটি সাব অ্যারে যার সাইজ 4, ইনডেক্স 5 থেকে 8 পর্যন্ত একটি সাব অ্যারে যার সাইজ 4।
এবার যেহেতু আমরা 4 দৈর্ঘ্যের সকল সাব অ্যারের মিনিমাম আগেই বের করে নিবো, তাই আমরা সাধারণ ভাবে লিখতে পারি,
এখানে আমরা আগের সারি বা কে নিয়ে কাজ করেছি কারণ সাইজের একটি সাব অ্যারেকে উপস্থাপন করে যা এর অর্ধেক।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 | #include<bits/stdc++.h> using namespace std; int main(){ int n=9; int arr[]={1,-2,4,3,-5,6,3,-82,-22}; int Maxk=__lg(n); // সর্বোচ্চ log_2(n) টি সারি বা k হতে পারে। int lookUpTable[Maxk+1][n]={{0}}; // এখানে আমরা রেঞ্জ মিনিমাম হিসাব করে জমা করবো। for(int k=0;k<=Maxk;k++){ // সারি বা k বরাবর লুপ, k পর্যন্ত চলবে। int subArraySize=1<<k; // 1<<k যেকথা 2^k একই কথা। k তম সারিতে সাব অ্যারের সাইজ 2^k // আমরা column+subArraySize-1<n এর মাধ্যমে বুঝতে পারবো n সাইজের অ্যারে তে subArraySize আকারের কয়টি সাব অ্যারে হতে পারে। // -1 এর কারণ আমরা ০ ভিত্তিক ইন্ডেক্সিং করেছি। for(int column=0;column+subArraySize-1<n;column++){ if(k==0){ // প্রথম সারিতে k=0, তাই প্রতিটি ইনডেক্স ই সাব অ্যারে হিসেবে বিবেচিত হবে। lookUpTable[k][column]=arr[column]; }else{ int next=column+(1<<(k-1)); // subArraySize এর একটা সাব অ্যারে, যেখানে subArraySize ২ এর একটি সূচকীয় মান, একে আমরা column থেকে 2^(k-1) //এবং next=column+(1<<(k-1)) থেকে 2^(k-1) এ ভাগ করতে পারি। lookUpTable[k][column]=min(lookUpTable[k-1][column],lookUpTable[k-1][next]); // ভাগ করা দুইতই সেগমেন্ট এর মিনিমাম। } } } } |
স্পার্স টেবিলে কুয়েরি করা (Query in sparse table Bangla tutorial)
স্পার্স টেবিলে কুয়েরি করা সহজ। শুধু একটি কনসেপ্ট বুঝতে হবে। ধরা যাক আমাদেরকে একটি রেঞ্জ এর মিনিমাম বের করতে দিলো। তো আমরা যা করবো প্রথমে বের করবো বা মোট যতগুলো ইলিমেন্ট আছে এই লেন্থে তার 2 ভিত্তিক লগ বের করে করে নিবো। এবার বুঝার চেষ্টা করি, এমন একটি সাব অ্যারের দৈর্ঘ্য যার মিনিমাম আমরা আগেই হিসাব করে নিয়েছি (যেহেতু r-l+1<=n) এবং ।
এখানে যেহেতু এর থেকে সমান অথবা বড় হবে এবং এর সমান বা ছোট হবে তাই বলতে পারি লেন্থের দুইটি সাব-অ্যারে নিয়ে আমরা কুয়েরি করলে রেঞ্জের সকল ইলিমেন্ট কভার করা যাবে। নিচের চিত্রটি দেখি।
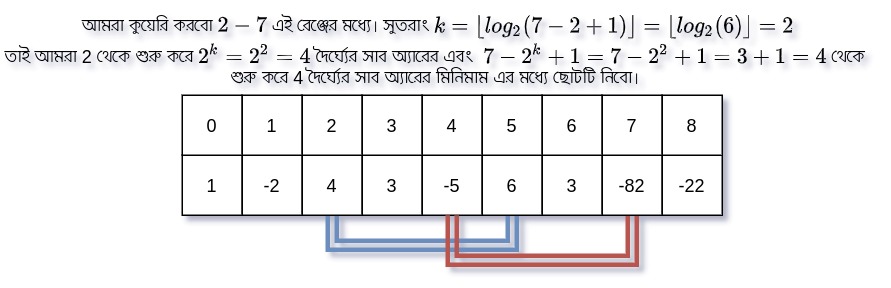
এখানে হলে । এখানে k=2 মানে আমরা দৈর্ঘ্যের সাব অ্যারের মিনিমাম বের করবো যা (১) l থেকে শুরু হয়েছে এবং যা (২) থেকে শুরু হয়েছে। এবার প্রথম সাব অ্যারে যা থেকে শুরু হয়েছে তা তো বুঝলাম। কিন্তু থেকে দৈর্ঘ্যের সাব অ্যারে কেন নিবো? লক্ষ করি, আমরা কিন্তু এর বাইরের কোন ইলিমেন্ট বিবেচনা করবো না। তাই আমাদেরকে দ্বিতীয় সাব অ্যারের এমন শুরুর ইনডেক্স বের করতে হবে যাতে সেখান থেকে দৈর্ঘ্যের সাব অ্যারে নিলে তা এ গিয়ে শেষ হয়, কারণ মিনিমাইজেশন প্রবলেমের ক্ষেত্রে অভারলেপিং ইলিমেন্ট নিলে সমস্যা নেই কিন্তু বাইরের ইলিমেন্ট নিলে সমস্যা রয়েছে।
আমরা এক লাইনেই কুয়েরি করতে পারি। কুয়েরি করার জন্য কে ইনপুট নিতে হবে।
| 1 | int num=min(lookUpTable[k][l],lookUpTable[k][r-(1<<k)+1]); |
নিচের কোডটি দিয়ে রেঞ্জে আমরা কুয়েরি করতে পারবো। [1<<k যেই কথা একই কথা]
| 1 2 3 4 5 | int l,r; cin>>l>>r; int k=__lg(r-l+1); int num=min(lookUpTable[k][l],lookUpTable[k][r-(1<<k)+1]); cout<<num<<endl; |
এটাই আমাদের সম্পূর্ণ স্পার্স টেবিলের টিউটোরিয়াল। আমরা খুব সহজেই কুয়েরি করে নিয়েছি সূত্র মেনে। প্রতিটি কুয়েরি সময় নিবে টাইম। যদিও বের করতে সময় লাগবে। আমরা ইচ্ছে করলে কুয়েরি করার লুপের বাইরে নিচের কোড দিয়ে 1 থেকে n পর্যন্ত সকল সংখ্যার এর মান এ হিসেব করে নিতে পারি।
| 1 2 3 4 | int log[n+1]; log[1] = 0; for (int i = 2; i <= n; i++) log[i] = log[i/2] + 1; |
তারপর আমরা int k=__lg(r-l+1);কে শুধু int k=log[r-l+1];দ্বারা এ বের করতে পারবো।
সম্পূর্ণ স্পার্স টেবিলের C++ কোড (Sparse table C++ implementation)
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 | #include<bits/stdc++.h> using namespace std; int main(){ int n=9; int arr[]={1,-2,4,3,-5,6,3,-82,-22}; int Maxk=__lg(n); // সর্বোচ্চ log_2(n) টি সারি বা k হতে পারে। int lookUpTable[Maxk+1][n]={{0}}; // এখানে আমরা রেঞ্জ মিনিমাম হিসাব করে জমা করবো। for(int k=0;k<=Maxk;k++){ // সারি বা k বরাবর লুপ, k পর্যন্ত চলবে। int subArraySize=1<<k; // 1<<k যেকথা 2^k একই কথা। k তম সারিতে সাব অ্যারের সাইজ 2^k // আমরা column+subArraySize-1<n এর মাধ্যমে বুঝতে পারবো n সাইজের অ্যারে তে subArraySize আকারের কয়টি সাব অ্যারে হতে পারে। // -1 এর কারণ আমরা ০ ভিত্তিক ইন্ডেক্সিং করেছি। for(int column=0;column+subArraySize-1<n;column++){ if(k==0){ // প্রথম সারিতে k=0, তাই প্রতিটি ইনডেক্স ই সাব অ্যারে হিসেবে বিবেচিত হবে। lookUpTable[k][column]=arr[column]; }else{ int next=column+(1<<(k-1)); // subArraySize এর একটা সাব অ্যারে, যেখানে subArraySize ২ এর একটি সূচকীয় মান, একে আমরা column থেকে 2^(k-1) //এবং next=column+(1<<(k-1)) থেকে 2^(k-1) এ ভাগ করতে পারি। lookUpTable[k][column]=min(lookUpTable[k-1][column],lookUpTable[k-1][next]); // ভাগ করা দুইতই সেগমেন্ট এর মিনিমাম। } } } int log[n+1]; log[1] = 0; for (int i = 2; i <= n; i++) log[i] = log[i/2] + 1; while(true){ int l,r; cin>>l>>r; int k=__lg(r-l+1); int num=min(lookUpTable[k][l],lookUpTable[k][r-(1<<k)+1]); cout<<num<<endl; } return 0; } |
আজকের লিখা এ পর্যন্তই সমাপ্ত রাখলাম। স্পার্স টেবিল আমার নিজের কাছে একটু জটিল লাগে। তাই আমি সাজেস্ট করবো লিখাটিতে আরও কয়েকবার চোখ বুলিয়ে নিতে। এতে করে অনেক ছোট ছোট বিষয়ে ধারনা পরিষ্কার হয়ে যাবে। #happy_coding.
স্পার্স টেবিল অনুশীলনের জন্য কিছু প্রবলেম (Credit: cp-algorithms.com)
- SPOJ – RMQSQ
- SPOJ – THRBL
- Codechef – MSTICK
- Codechef – SEAD
- Codeforces – CGCDSSQ
- Codeforces – R2D2 and Droid Army
- Codeforces – Maximum of Maximums of Minimums
- SPOJ – Miraculous
- Codeforces – Animals and Puzzles
- Codeforces – Trains and Statistics
- SPOJ – Postering
- SPOJ – Negative Score
- SPOJ – A Famous City
- SPOJ – Diferencija
- Codeforces – Turn off the TV
- Codeforces – Map
- Codeforces – Awards for Contestants
- Codeforces – Longest Regular Bracket Sequence