লেজি প্রপাগেশন (Lazy propagation)
ধরেন আপনাকে একটা Array দেয়া হলো arr[] = [1,2,3,4,5,6,7,8]। পরে বলা হলো আপনাকে Q সংখ্যক কুয়েরি করা হবে। প্রতি টি কুয়েরিতে প্রথমে, একটা ইনডেক্সে আপডেট করবেন এবং পরে তার আউটপুট বলতে হবে। এর এফিসিয়েন্ট সলুশন করা যায় সেগমেন্ট ট্রি ডাটা স্ট্রাকচার দিয়ে যা এই পোস্টে পাবেন। যারা পোস্টটি দেখেন নি আগে দেখে নেওয়ার অনুরোধ রইলো। নাহলে লেজি প্রপাগেশন বুঝতে একটু সমস্যা হতে পারে।
এখন আরেক দৃশ্য দেখা যাক। ধরেন আপনার কাছে arr[] = [1,2,3,4,5,6,7,8] আছে। আপনাকে Q টা কুয়েরিই করা হবে। কিন্তু এক্ষেত্রে আপনাকে দুটি কাজ করতে হবে।
- আপডেট: arr[] এর l থেকে r রেন্জে একটি ভ্যালু x দ্বারা আপডেট করতে হবে।
- কুয়েরি: arr[] এর l থেকে r রেন্জের সংখ্যাগুলোর যোগফল প্রিন্ট করতে হবে
লেজি প্রপাগেশন বাংলা টিউটোরিয়াল
এর একটি সলূশন হতে পারে l থেকে r এর প্রতিটি ইনডেক্সের নোড এ গিয়ে আমরা আমাদের ভ্যালু (value) দিয়ে আপডেট করবো। পরে আমরা সাধারণ সেগমেন্ট ট্রিতে কুয়েরির মতো করে প্রিন্ট করে দিবো। কিন্তু এক্ষেত্রে লক্ষ করলে দেখা যায় প্রতিবার আপডেটে আমাদের টাইম কমপ্লেক্সিটি দাড়ায় O(N) এ। সুতরাং Q বার আপডেট করার পরে তা হবে O(Q.N), যাকে সহজেই O(N^2) করা যাবে। তো এখন উপায় কি?
আমরা উপরের সমস্যাটিকে সেগমেন্ট ট্রি ডাটা স্ট্রাকচার এর লেজি প্রপাগেশন নামক একটি পদ্ধতি অনুসরন করে সহজেই log(n) প্রতি আপডেটে, করতে পারি। আজকের আলোচনার টপিক এইটাই (লেজি প্রপাগেশন)।
এক্ষেত্রে আমরা যা করবো তা সহজে বলতে গেলে দাড়ায়, আমরা প্রতিটি নোডে না গিয়ে উপরেই আমাদের রিলেভেন্ট নোডে (যেই নোড কুয়েরি রেন্জের মধ্যে আছে) লিখে রাখবো। এই যে লিখে রাখলাম, একেই আমরা লেজি (Lazy) বলি। এটা করার পরে এখন আর আমাদের নিচের নোডে নামতে হবে না। কুয়েরি করার সময় আমরা কিছু হিসাব করেই উত্তর বলে দিতে পারবো।
সুতরাং বুঝতেই পারছেন, এই ট্রি টি বিল্ট করতে হলে আমাদেরকে Lazy এর মান লিখে রাখার জন্যে অবশ্যই একটি অপশন রাখা লাগবে। আমাদের এই লেখায় আমরা স্ট্রাকচার (struct) ব্যবহার করে ট্রি টি বানাবো। তাই আমরা স্ট্রাকচার এর গঠনটা একটু দেখে নিই:
| 1 2 3 4 | struct node{ int value=0; int lazy=0; }; |
কোডে লক্ষ করলে দেখতে পারবেন আমরা স্ট্রাকচারে ২টি ইন্টিজার ভ্যারিয়েবল নিয়েছি। এদের মধ্যে একটি হলো value যা ব্যবহার হবে নোড ভ্যালু লিখে রাখার জন্যে, আর lazy নামক ভ্যারিয়েবলটা ব্যবহার হবে ঐ নোডে এ পর্যন্ত কি পরিমান আপডেট হয়েছে তা লিখে রাখার জন্যে। এখন আমরা আমাদের ট্রি টি বিল্ড করবো।
লেজি প্রপাগেশন: সেগমেন্ট ট্রি বিল্ড করা
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | void build(int L,int R,int at){ if(L==R){ tree[at].value=arr[L]; return; } int mid=(L+R)/2; int left = 2*at; int right=2*at+1; build(L,mid,left); build(mid+1,R,right); tree[at].value+=tree[left].value+tree[right].value; } //call it using build(0,arraySize-1,1); |
এই বিল্ড কোডটির সাথে আগে দেখানো সেগমেন্ট ট্রি এর বিল্ড কোডের তফাৎটুকু হলো যে, এখানে যেহেতু tree এর নোড গুলো হলো স্টাকচার, তাই এখানে আমাদের ভ্যালুগুলো স্ট্রাকচার এর value ভ্যারিয়েবল এ যোগ করতে হচ্ছে।
বিল্ড কোডটি একটু বুঝিয়ে বলা যাক। build() ফাংশনটি যা প্যারামিটার হিসেবে গ্রহন করবে তা হলো, অ্যারে এর শুরুর ইনডেক্স (L), অ্যারে এর শেষ ইনডেক্স (R), tree এর বর্তমান নোড ইনডেক্স (at)।
এখানে প্রথম কন্ডিশন if(L==R), এইটা হলো বেস কেস, মানে এসময় আমরা আমাদের অ্যারে এর উপাদান গুলিকে সরাসরি ট্রি তে ঐ নোড এ ঢুকিয়ে দিতে পারবো। এখানে আমরা ট্রিতে ঐ নোডের value ভ্যারিয়েবল এ অ্যারের উপাদানটিকে ঢুকিয়ে দিয়েছি।
L==R হলে আমরা যে নোড গুলাতে থাকবো, সেই নোড গুলো একেকটা লিফ (leaf) নোড। এই নোডগুলোতে একটা করে উপাদান থাকবে। উপাদান গুলো হলো মূল অ্যারে arr[] এর প্রতিনিধি।
| 1 | tree[at] = arr[L] |
তা না হলে আমরা পুনরায় অ্যারেটিকে দুইভাগে ভাগ করে নিয়েছি। এবং পুনরায় রিকার্সিভ কল করার মাধ্যমে লেফ্ট ও রাইট নোড ভিজিট করেছি যতক্ষন না L=R হয়। সবশেষে আমরা আমাদের বর্তমান নোড এর ভ্যালুটিতে বামের নোড এবং ডানের নোড এর যোগফল ঢুকিয়েছি। বাম এবং ডানের নোড এর ভ্যালু টি আমরা রিকার্সিভ কল করার মাধ্যমে পেয়েছি
| 1 | tree[at].value+=tree[left].value+tree[right].value; |
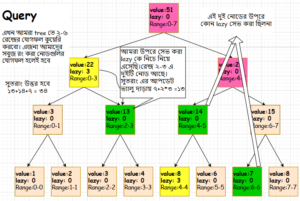
ট্রি টি কে আমরা চিত্রের মাধ্যমে দেখেনেই।
আমরা রেফারেন্স অ্যারে হিসেবে [1,2,3,4,5,6,7,8] ব্যবহার করেছি।
লেজি প্রপাগেশন: সেগমেন্ট ট্রি আপডেট করা
এতক্ষন যা দেখলাম তা হলো tree বিল্ড করার কোড। এবার দেখবো রেন্জ l ও r কে আপডেট করার পদ্ধতি। আগেই বলা হয়েছিলো আপডেট করার সময় আমরা প্রত্যেকটি নোড এ গিয়ে আপডেট না করে রিলেভেন্ট নোড এ লিখে রাখবো। এই অংশটি একটু ভালো ভাবে খেয়াল করতে হবে।
প্রথমেই আমরা দেখবো যে আমরা বর্তমানে যেই নোড এ আছি তা যেই রেন্জে আপডেট করবো সেই রেন্জে পরে কি না। মানে আমাদের দেখতে হবে, বর্তমানে যে রেন্জে আছি (L,R) তা পুরোপুরি বা আংশিক ভাবে আমাদের দেয়া রেন্জ (l,r) কে কভার করে কি না। যদি পরে তবে আমরা আর নিচে নামবো না। ঐ নোডেই lazy ভ্যারিয়েবল এ লিখে রাখবো যে, এই নোডের যত গুলো চাইল্ড নোড আছে সেখানে একটি মান x যোগ হবে। একই সাথে আমরা ঐ নোডের যে value ভ্যারিয়েবলটি আছে, সেখানে একটি মান রাখবো যা হবে সবগুলো লিফ নোড আসলেই আপডেট করা হলে যে মান পাওয়া যেত তা। এক্ষেত্রে আমাদের ভ্যালুর মানটি হবে, (ঐ নোডের মোট লিফ নোডের সংখ্যা)*x বা (R-L+1)*x । তাহলে এখন আপডেট করার কোডটি দেখে নেওয়া যাক।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | void update(int l,int r,int x,int L,int R,int at){ if(l>R||r<L) return; if(L>=l&&R<=r){ tree[at].value+=(R-L+1)*x; tree[at].lazy+=x; return; } int mid = (L+R)/2; int left = at*2; int right = at*2+1; update(l,r,x,L,mid,left); update(l,r,x,mid+1,R,right); tree[at].value = tree[left].value+tree[right].value+(R-L+1)*tree[at].lazy; } //call it using update(l,r,x,0,arraySize-1,1) |
এখানে প্রথম কন্ডিশন if(l>R||r<L) এ দেখা হয়েছে আমরা বর্তমানে যে নোডে আছি তা কি আমাদের দেয়া, l ও r এর বাইরে কিনা। যদি বাইরে থাকে তবে আমাদের আর নিচে যাওয়ার প্রয়োজন নাই। তারপরের if(L>=l&&R<=r) এই কন্ডিশনে দেখা হয়েছে আমরা এখন যেই নোডে অবস্থান করছি তা আমাদের দেওয়া l এবং r এর মধ্যে আছে কিনা। যদি মধ্যে থাকে তবে আমরা ঐ নোডে গিয়ে আমাদের দেওয়া তথ্য গুলো লিখে রেখে আসবো।
| 1 2 | tree[at].value+=(R-L+1)*x; tree[at].lazy+=x; |
এখানে প্রথম লাইনে, tree[at].value তে আমরা যে ভ্যালুটা যোগ করেছি তা হলো এর নিচে যতগুলো লিফ নোড আছে তাদের আপডেট করার পরে মোট যেটুকু বাড়তো তা। আর পরের লাইনে lazy ভ্যালু আপডেট করা হয়েছে। আমরা x যোগ করার মাধ্যমে এটা বলে দিয়েছি যে এখন পর্যন্ত এই নোডের লিফগুলোতে lazy+x যোগ করার কথা হয়েছ। এই কাজটি আমাদের করতে হয়েছে তার কারন হলো যদি কুয়েরি করার সময় আমাদের কোন কারনে আমাদের আরও নিচের নোডে নামতে হয় তবে আমরা lazy ভ্যালু নিচে নিয়ে যাবো এবং হিসাব করবো (যেহেতু আমরা ঐ নোডের নিচে কোন আপডেট করিনি। যা করার উপরে করেই ফেরত গিয়েছি)।
এবার, নিচের লাইনগুলোতে শুধু build ফাংশনের মতোই ডান আর বামের নোডে ভিজিট করা হয়েছে। সবশেষে উপরে উঠার সময় শেষ লাইনে ডান আর বাম নোডের যোগফলগুলো আর বর্তমান নোডের Lazy ভ্যালু দিয়ে বর্তমান নোড আপডেট করা হয়েছে।
চিত্রের মাধ্যমে একটি উদাহরণ দেই
এখানে আমরা tree এর ০ থেকে ৩ রেন্জে ৩ যোগ করবো। এখানে আমাদের শুধু হলুদ রং করা নোড গুলোতে lazy ভ্যালুটি সেভ করে রাখতে হবে (কোডের ৪ ও ৫ নং লাইন) । একই সাথে গোলাপী রং করা প্যারেন্ট গুলোকে আপডেটেড ভ্যালু দিয়ে আপডেট করতে হবে (কোডের ১৩ নং লাইন)।
এবার আসি কুয়েরি করার বেলায়। এখন প্রশ্ন আসে যে আমরা তো নোড গুলোতে Lazy ভ্যালু লিখে দিয়েই আমাদের কার্য উদ্ধার করেছি। তবে আমরা কুয়েরি করবো কিভাবে?
লেজি প্রপাগেশন: সেগমেন্ট ট্রি তে কুয়েরি করা
আপনারা যদি আগের আটিকেলটা পরেন তবে এই সিস্টেমটা আপনার জন্য বুঝা খুবই সহজ হয়ে যাবে। শুধু এখানে আমাদের আলাদা একটা প্যারামিটার নেয়ার দরকার হবে, যা উপরের নোডগুলো থেকে Lazy ভ্যালু গুলোর যোগফল নিচের নোডগুলোতে নিয়ে যাবে। আমরা এই প্যারামিটারটির নাম দিলাম carry. চলেন কোডটা দেখে নেই।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | int query(int l,int r,int L,int R,int at,int carry){ if(l>R||r<L) return 0; if(L>=l&&R<=r){ return tree[at].value+carry*(R-L+1); } int mid = (L+R)/2; int left=at*2; int right=at*2+1; int carryValue = carry+tree[at].lazy; int x = query(l,r,L,mid,left,carryValue); int y = query(l,r,mid+1,R,right,carryValue); return x+y; } //call it using query(l,r,0,arraySize-1,1,0) |
এখানে l এবং r হলো আমাদের কুয়েরি রেন্জ। L এবং R হলো অ্যারের নিচের ইনডেক্স আর উপরের ইনডেক্স। at হলো বর্তমান নোড ইনডেক্স যা শুরুতে ১। carry হলো Lazy ভ্যালুগুলোকে নিচে নিয়ে যাওয়ার জন্য প্রয়োজনীয় প্যারামিটার।
এখানে প্রথম কন্ডিশনে শুধু দেখা হয়েছে বর্তমানে যে নোডে আছি তা রিলেভেন্ট কিনা। যদি রিলেভেন্ট না হয় তবে নিচে নামার কোন দরকার নেই। আর পরের কন্ডিশনে চেক করা হয়েছে বর্তমান নোড এর রেন্জ l এবং r এর মধ্যে কিনা। মধ্যে হলে আমরা আমাদের হিসাব রিটার্ন করেছি। হিসাব এর অংশটুকু বুঝার আগে আমাদের ৯ নং লাইনে একবার চোখ বুলিয়ে নেই।
| 1 | int carryValue = carry+tree[at].lazy; |
এই লাইনে যা করা হয়েছে তা হলো, আমরা উপর থেকে নিচের নোডে যাওয়া পর্যন্ত যেসব নোডে Lazy সেভ করে রেখেছি তা carry প্যারামিটার দিয়ে নিচে এনেছি। এখন আবার আমাদের carry হিসাব করতে হবে। ধরি নতুন করে carry ভ্যালুতে যোগ হবে u. তহেলে u=tree[at].lazy। এবং নতুন carry ভ্যালু হবে carry+u. এবার চলেন ৩ নং লাইনে যাই।
| 1 | return tree[at].value+carry*(R-L+1); |
এখানে আমরা আমাদের নোডে যে ভ্যালু আগে থেকেই ছিলো তার সাথে উপরের নোডগুলো থেকে বয়ে আনা carry ভ্যালুর জন্য যে ভ্যালু পেতাম তার যোগফল রিটার্ন করেছি।
Why the carry parameter?
এখন আসি আমরা কিজন্য carry প্যারামিটার নিলাম। কারন, আমরা আপডেট করার সময় শুধু উপরের নোডগুলোতেই আপডেট করেছি এবং lazy ভ্যারিয়েবল এ তা লিখে রেখেছি। কিন্তু নিচে কোন আপডেট হয় নাই। যেহেতু উপরে আপডেট হয়েছে, তাই এজন্য এর প্রভাব নিচে কতখানি পরতো তাই carry ভ্যারিয়েবল এর সহায়তায় বের করেছি।
চিত্রের মাধ্যমে একটি উদাহরণ দেই
প্রথম সবুজ রং করা নোডটিকে খেয়াল করি।
সব মিলিয়ে কোডটা দাড়ায় নিম্নরুপ:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 | /* Sharif Hasan - CSE, PUST Apr 07, 2020 11: 19 AM */ //Lazy propagation bangla tutorial //Input any 8 numbers #include<bits/stdc++.h> #define br cout<<"\n" using namespace std; #define mx 8 struct node{ int value=0; int lazy=0; }; int arr[mx]; node tree[mx*4]; void build(int L,int R,int at){ if(L==R){ tree[at].value=arr[L]; return; } int mid=(L+R)/2; int left = 2*at; int right=2*at+1; build(L,mid,left); build(mid+1,R,right); tree[at].value+=tree[left].value+tree[right].value; } //call it using build(0,arraySize-1,1); void update(int l,int r,int x,int L,int R,int at){ if(l>R||r<L) return; if(L>=l&&R<=r){ tree[at].value+=(R-L+1)*x; tree[at].lazy+=x; return; } int mid = (L+R)/2; int left = at*2; int right = at*2+1; update(l,r,x,L,mid,left); update(l,r,x,mid+1,R,right); tree[at].value = tree[left].value+tree[right].value+(R-L+1)*tree[at].lazy; } //call it using update(l,r,x,0,arraySize-1,1) int query(int l,int r,int L,int R,int at,int carry){ if(l>R||r<L) return 0; if(L>=l&&R<=r){ return tree[at].value+carry*(R-L+1); } int mid = (L+R)/2; int left=at*2; int right=at*2+1; int carryValue = carry+tree[at].lazy; int x = query(l,r,L,mid,left,carryValue); int y = query(l,r,mid+1,R,right,carryValue); return x+y; } //call it using query(l,r,0,arraySize-1,1,0) /*Main function*/ int main() { int i; for(i=0;i<mx;i++){ cin>>arr[i]; } build(0,mx-1,1); update(0,4,3,0,mx-1,1); cout<<query(2,6,0,mx-1,1,0);br; return 0; } |
মুটামুটি এই ছিলো আমাদের লেজি প্রপাগেশন কাহিনি। মুলত লেজি প্রপাগেশন ছাড়া সেগমেন্ট ট্রি অচল। লেজি প্রপাগেশন আপনি আরও অনেক উপায়ে করতে পারেন। নিচে আপনাদের প্রাক্টিস করার জন্য কিছু প্রবলেম এর লিংক দিলাম
For further reading Time Complexity.
আজকের এই লেখাটি আমি আমাদের A.H. Himon ভাইকে উৎসর্গ করলাম। তিনি আমাকে লেজি প্রপাগেশন শেখাতে খুব পরিশ্রম করেছেন। ধন্যবাদ ভাই ❤️।
Special thanks to Abrar Nafee Akhand
আর্টিকেলটি কেমন লাগলো জানাবেন। যদি কোন স্থানে বুঝতে সমস্যা হয় তবে,নিশ্চিন্তে কমেন্ট করুন।





খুব ভালো হইছে ভাই। নেক্সট পোস্ট খুব দ্রুত পাব আশা করি ❤️।
ধন্যবাদ ভাইয়া। ইনশাআল্লাহ্ খুব দ্রুত পাবেন ❤️❤️
ডাটা স্ট্রাকচার নিয়ে এমন আরো পোস্ট চাই
পাবেন আশা করি
Well done brother 💜
Really helpful and very easy to understand 💜
ধন্যবাদ সাদী। চেস্টা করেছি ভালো করে লেখতে।
bhai onk dhonnobad ..
khub easily bujte parlam bhai