গ্রাফ কি?
গ্রাফ (Graph) হলো একটি গুরুত্বপূর্ণ ডাটা স্ট্রাকচার যা দুইটি অবজেক্ট এর মধ্যে রিলেশন উপস্থাপন করতে ব্যবহার করা হয়। এই অবজেক্টগুলো হতে পারে, কোনও শহর/নেটওয়ার্ক এ কোনও মোবাইল ফোন ইত্যাদি। গ্রাফের দুইটি বেসিক কম্পনেন্ট হলো নোড এবং এজ।
নোড এবং এজ
নোড বা ভারটেক্স (Nodes/vertex): আমরা যদি গ্রাফ কে কয়েকটি শহরের সংযোগ হিসেবে ধরি তবে শহরগুলো হবে নোড বা ভার্টেক্স।
এজ (Edge): এজ হলো গ্রাফের একটি গুরুত্বপূর্ণ কম্পোনেন্ট যার মাধ্যমে আমরা দুইটি নোড এর রিলেশন উপস্থাপন করতে পারি। সোজা বাংলায় বলতে গেলে, গ্রাফ এর এজ হলো দুইটি নোড এর সংযোগ। এজ গুলো ব্যবহার করে আমরা একটি নোড থেকে আরেকটি নোড এ যেতে পারি। অ্যাডজাসেন্ট নোড (Adjacent node): একই এজ দিয়ে সংযুক্ত দুইটি নোড কে আডজাসেন্ট নোড বলে। নিচের চিত্রে ১ নং নোড ও ২ নং নোড হলো অ্যাডজাসেন্ট নোড। একই ভাবে ২ নং নোড এবং ৩ নং, ২ নং ও ৪ নং,৪ নং ও ৬ নং ইত্যাদি অ্যাডজাসেন্ট নোড।
টেলিফোন নেটওয়ার্ক,কোনও শহরের সাথে শহরের সংযোগ, সার্কিট ইত্যাদি গ্রাফ ব্যবহার করে খুব সহজে উপস্থাপন করা যায়। বিভিন্ন সোসাল মিডিয়া সাইট গুলোতেও গ্রাফ এর ব্যবহার করে সহজে ডাটা খুজে বের করা হয়। যেমন, Facebook এ প্রত্যেক ব্যাক্তি একেকটি নোড বা ভার্টেক্স। এর একেকটি নোড এ ID,Name,Gender,Age ইত্যাদি জমা থাকে। এই নোড গুলোর সাথে আরও নোড কানেকটেড (Connected) থাকে।
নিচে চিত্রের মাধ্যমে একটি গ্রাফ দেখানো হলোঃ
ডিরেক্টেড গ্রাফ এবং আনডিরেক্টেড গ্রাফঃ
ডিরেক্টেড গ্রাফঃ উপরের গ্রাফটি কে যদি আমরা অ্যারো (→) দিয়ে বলে দেই কোন নোড থেকে কোন নোড এ যেতে পারা যাবে আর কোথায় যাওয়া যাবে না তবে গ্রাফটি ডিরেক্টেড গ্রাফ হয়ে যাবে।
উপরের গ্রাফটি একটি ডিরেক্টেড গ্রাফ। এই গ্রাফে আমরা নোড ১ থেকে নোড ২ এ যেতে পারি কিন্তু ২ থেকে ১ এ যেতে পারবোনা আমরা। একই ভাবে আমরা ২ থেকে ৩ এবং ২ থেকে ৪ এ যেতে পারবো। কিন্তু ৪ থেকে ২ এ যেতে পারবো না।
আনডিরেক্টেড গ্রাফঃ এই ধরেনের গ্রাফের নোড গুলোর রাস্তায় কোনও দিক নির্দিষ্ট করা থাকে না। এখানে আমরা এক নোড থেকে আরেক নোড এ যে রাস্তায় যেতে পারি আবার ঐ একই রাস্তায় আবার আগের নোড এ ফেরত যেতে পারি। সবার প্রথমে আমরা যে গ্রাফটি দেখেছি তা একটি আনডিরেক্টেড গ্রাফ।
ওয়েটেড (Weighted) গ্রাফ এবং আনওয়েটেড (Unweighted) গ্রাফঃ
অনেক সময় গ্রাফে এজগুলোর পাশে ছোট করে ওয়েট বা কস্ট (Cost) লিখা থাকতে পার। এই ওয়েট গুলো দ্বারা অনেক কিছু বুঝাতে পারে। যেমন দুইটি শহরের মধ্যে দূরত্ব/রাস্তা টি দিয়ে যেতে কতটুকু সময় লাগে ইত্যাদি। নিচের চিত্রটি হলো একটি ডিরেক্টেড ওয়েটেড গ্রাফ।
এখানে ১ থেকে ২ এ যেতে আমাদের কস্ট হলো ৩। ২ থেকে ৩ এ যেতে কস্ট হলো ৬। ৭ থেকে ৩ এ যেতে কস্ট ১।
অপর দিকে আগে যেই গ্রাফগুলো দেখেছি তা হলো আনওয়েটেড গ্রাফ। এক্ষেত্রে আমরা সবগুলো এজ এর কস্ট ১ ধরে নেই।
গ্রাফ এর রিপ্রেজেন্টেশন
গ্রাফ এর রিপ্রেজেন্টেশন এর জন্য সাধারণত নিচের দুইটি পদ্ধতি ব্যবহার করা হয়ঃ
- অ্যাডজেসেন্সি লিস্ট (Adjacency list)।
- অ্যাডজেসেন্সি ম্যাট্রিক্স (Adjacency matrix)।
অ্যাডজেসেন্সি ম্যাট্রিক্স
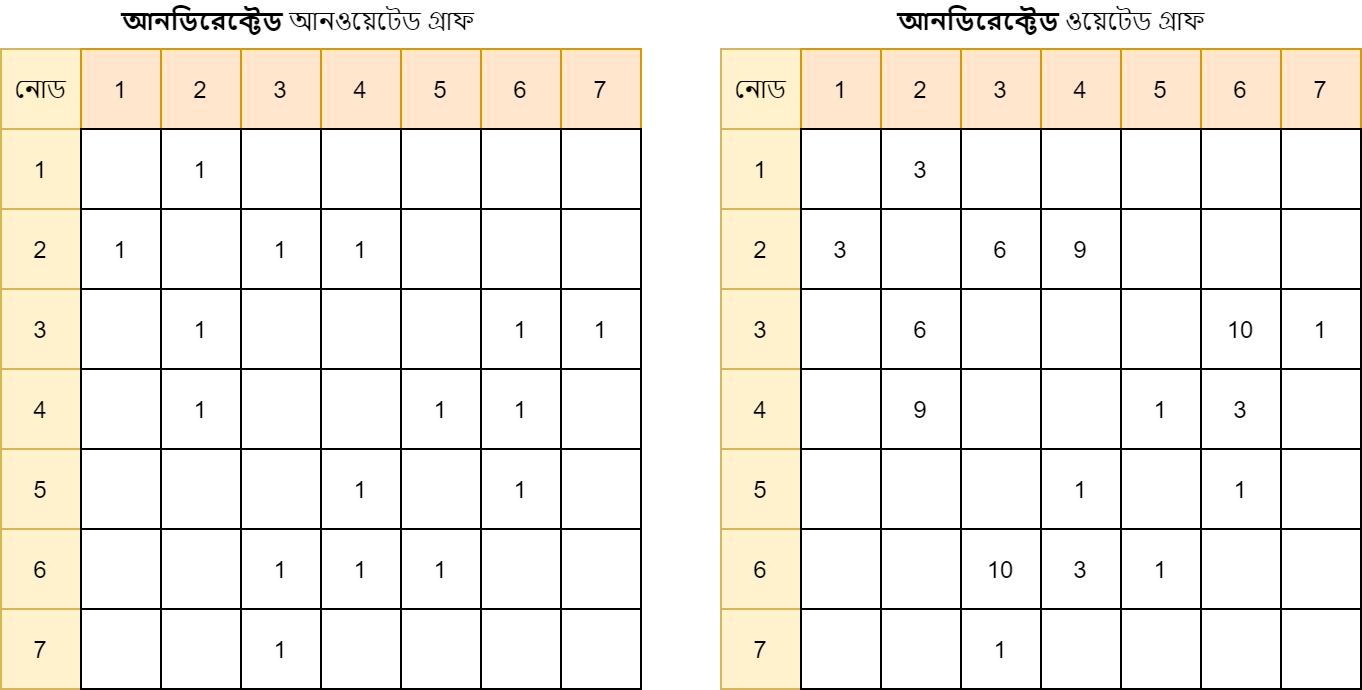
আমরা উপরে অ্যাডজাসেন্ট নোড এর ধারনা দেখে এসেছি। অ্যাডজাসেন্সি ম্যাট্রিক্স এর ধারনাটিও খুব সহজ। প্রথমে আমরা একটা 2D অ্যারে নিবো। যদি যেকোনো নোড i এবং j এর মধ্যে এজ থাকে তবে ডিরেক্টেড গ্রাফ এর জন্য অ্যারের i তম রো এবং j তম কলাম এর মান 1 করে দিবো। আনডিরেক্টেড গ্রাফ এর জন্য অ্যারের i তম রো, j তম কলাম এবং j তম রো, i তম কলাম আর এর মান 1 করে দিবো। যদি আমাদের এজ গুলো ওয়েটেড হয় তবে এখানে আমাদের ওয়েট বসাতে হবে। নিচের চিত্রটি দেখলে পরিষ্কার হয়ে যাবে।
উপরের ছক দুইটি আনডিরেক্টেড গ্রাফ এর জন্য অ্যাডজেসেন্সি মেটিক্স এর উপস্থাপন। ডিরেক্টেড গ্রাফ এর জন্য নিচের মতো হবে।
ইমপ্লিমেন্টেশন
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | /* Sharif Hasan - CSE, PUST May 04, 2020 09: 49 AM */ #include<bits/stdc++.h> using namespace std; /*Main function*/ int main() { int numberOfNode=7; int adjacencyMatrix[numberOfNode+1][numberOfNode+1]={{0}}; /* আমরা আমাদের অ্যাডজেসেন্সি ম্যাট্রিক্স এ এখন আমাদের গ্রাফ কে সেভ করবো*/ adjacencyMatrix[1][2]=adjacencyMatrix[2][1]=1; adjacencyMatrix[2][3]=adjacencyMatrix[3][2]=1; adjacencyMatrix[2][4]=adjacencyMatrix[4][2]=1; adjacencyMatrix[3][7]=adjacencyMatrix[7][3]=1; adjacencyMatrix[3][6]=adjacencyMatrix[6][3]=1; adjacencyMatrix[4][5]=adjacencyMatrix[5][4]=1; adjacencyMatrix[4][6]=adjacencyMatrix[6][4]=1; adjacencyMatrix[5][6]=adjacencyMatrix[6][5]=1; cout<<"নোড ২ এবং নোড ৩ এর মধ্যে নোড আছে কি না?\n"; if(adjacencyMatrix[2][3]){ cout<<"আছে\n"; }else{ cout<<"নাই\n"; } cout<<"নোড ৪ এবং নোড ৭ এর মধ্যে নোড আছে কি না?\n"; if(adjacencyMatrix[4][7]){ cout<<"আছে\n"; }else{ cout<<"নাই\n"; } return 0; } |
অ্যাডজেসেন্সি ম্যাট্রিক্স এর ভালো এবং খারাপ দিক
ভালো দিক
- রিপ্রেজেন্টেশন ইমপ্লেমেন্ট করা সহজ।
- একটি এজ মুছে দিতে O(1) সময় নেয়।
- দুইটি নোড এর মধ্যে এজ আছে কি না তা চেক করতে O(1) সময় লাগে।
খারাপ দিক
- স্পেস কমপ্লেক্সিটি বেশি ,O(N*N)।
- কোনও একটি নোড এর অ্যাডজাসেন্ট নোডগুলো বের করতে হলে N টি নোডই পরীক্ষা করে দেখতে হয়।
- ওয়েটেড গ্রাফে দুইটি নোড এর মধ্যে একাধিক এজ থাকলে আডজেসেন্সি ম্যাট্রিক্স দিয়ে তা উপস্থাপন সম্ভব না।
অ্যাডজেসেন্সি লিস্ট
অ্যাডজেসেন্সি লিস্ট হলো মূলত একটি লিস্ট এর অ্যারে। এখানে কোন নোড এর এর সাথে কোন নোড যুক্ত আসে তা একটি তালিকা আকারে প্রকাশ করা হয়। উপরের গ্রাফটির অ্যাডজেসেন্সি লিস্ট উপস্থাপন দেখা যাক
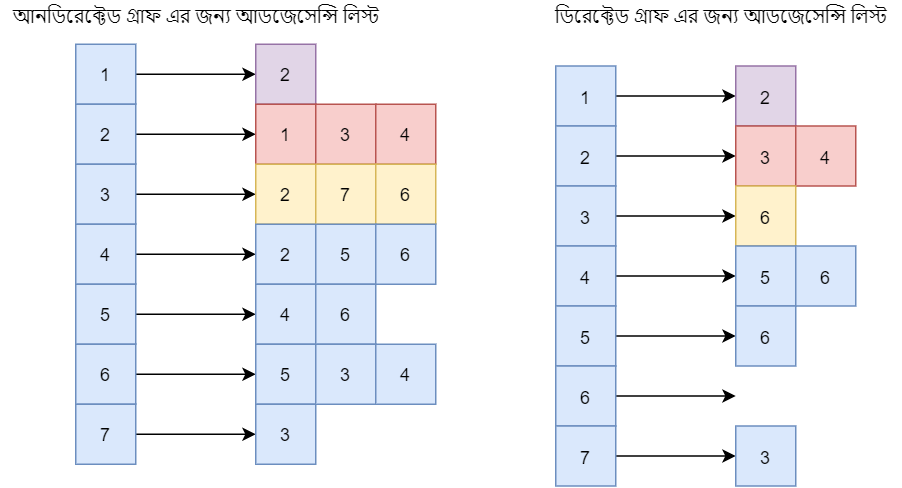
এখানে আনডিরেক্টেড গ্রাফ এর জন্য যেই আডজেসেন্সি লিস্টটি সেখানে লক্ষ করলে দেখা যায়, ১ নং ইনডেক্স এর লিস্ট এ ২ যেমন আছে তেমনি ২ নং ইনডেক্স এর লিস্ট এ ১ আছে। একই কথা বাকি নোড গুলোর জন্য প্রযোজ্য। অপর দিকে ডিরেক্টেড গ্রাফ এর জন্য যেই আডজেসেন্সি লিস্টটি সেখানে লক্ষ করলে দেখা যায় ১ থেকে ২ এ যাউয়া যায় বলে শুধু ১ নং ইনডেক্স এ লিস্ট এ ২ আছে, ২ নং ইনডেক্স এর লিস্ট এ ১ নাই। একই কথা বাকি নোড গুলোর জন্যও প্রযোজ্য।
ইমপ্লিমেন্টেশন
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 | /* Sharif Hasan - CSE, PUST May 04, 2020 09: 49 AM */ #include<bits/stdc++.h> using namespace std; /*Main function*/ int main() { int numberOfNode=7; vector <int> adjacencyList[numberOfNode+1]; adjacencyList[1].push_back(2); adjacencyList[2].push_back(1); adjacencyList[2].push_back(3); adjacencyList[2].push_back(4); adjacencyList[3].push_back(2); adjacencyList[3].push_back(7); adjacencyList[3].push_back(6); adjacencyList[4].push_back(2); adjacencyList[4].push_back(5); adjacencyList[4].push_back(6); adjacencyList[5].push_back(4); adjacencyList[5].push_back(6); adjacencyList[6].push_back(5); adjacencyList[6].push_back(3); adjacencyList[6].push_back(4); adjacencyList[7].push_back(3); cout<<"আমাদের অ্যাডজেসেন্সি লিস্টঃ\n"; for(int i=1;i<numberOfNode+1;i++){ for(int j=0;j<adjacencyList[i].size();j++){ cout<<adjacencyList[i][j]<<" "; } cout<<endl; } return 0; } |
অ্যাডজেসেন্সি লিস্ট এর ভালো এবং খারাপ দিক
ভাল দিক
- যতগুলো এজ আছে ঠিক তত মেমোরি ব্যবহার করেই আমরা গ্রাফ টি সেভ করে ফেলতে পারবো।
- একটি নোড এর সঙ্গে অ্যাডজাসেন্ট নোড কারা তা দেখার জন্য প্রতিটি নোড দেখার দরকার নেই। লিস্ট দেখলেই বলা যায়।
খারাপ দিক
- দুইটি নোড i,j এর মধ্যে এজ আছে কি না O(1) এ চেক করা পসিবল না। এজন্য লিস্ট এ লুপ চালাতে হবে।
গ্রাফ এর প্রয়োগ হয় কোথায়?
- কম্পিউটার সায়েন্স এর বিভিন্ন অ্যালগরিদম নিয়ে কাজ করতে গ্রাফ থিউরি ব্যবহার করা হয়
- Kruskal’s Algorithm
- Prim’s Algorithm
- Dijkstra’s Algorithm ইত্যাদি।
- ইলেক্ট্রিকাল ইঞ্জিনিয়ারিং গ্রাফ থিউরির কনসেপ্ট গুলো সার্কিট এর কানেকশন ডিজাইন করতে ব্যবহার করা হয়।
- কম্পিউটার নেটওয়ার্ক এ পরষ্পর যুক্ত কম্পিউটার গুলো গ্রাফ থিউরির প্রিন্সিপাল মেনে চলে।
- বিজ্ঞান− Molecular structure এবং Chemical structure, DNA structure গুলো গ্রাফ দিয়ে উপস্থাপন করা হয়।
আজকে এই পর্যন্তই রাখছি। কেমন হলো জানাবেন। পরবর্তী আর্টিকেল গুলো গ্রাফ থিউরির উপর লেখা হবে। তাই এই লেখাটিকে বলা যায় পরিবর্তি লেখাগুলোর শুরু। Happy coding.
আরো পড়ুন ট্রাই (প্রিফিক্স ট্রি/রেডিক্স ট্রি)। প্রোগ্রামিংঃ টেইল কল রিকার্শন অপটিমাইজেশন টেকনিক ।গ্রাফ থিওরিতে হাতেখড়ি – ১






অনেক ভালো হয়েছে।
গ্রাফের কিছুই জানতাম না, তারপরো বুঝতে পারেছি।
আচ্ছা একটা প্রশ্ন,
অ্যাডজেসেন্সি লিস্ট ব্যাবহার করে ওয়েটেড গ্রাফ represent করবো কি ভাবে।
std::pair ব্যবহার করা যেতে পারে। যেমন
pair aNode = make_pair(6,3);
adjacencyList[5].push_back(aNode);
এখানে নোড ৫ থেকে ৬ এ যাওয়ার weight ৩
https://stackoverflow.com/questions/54909372/adjacency-list-representation-of-a-weighted-graph
ওয়েটেড গ্রাফে দুইটি নোড এর মধ্যে একাধিক এজ থাকলে আডজেসেন্সি লিস্ট দিয়ে তা উপস্থাপন যায়?
হা করা যায়। আপনি স্ট্রাকচার ব্যবহার করতে পারেন সেক্ষেত্রে এজ এর ওয়েট সেভ রাখার জন্য।