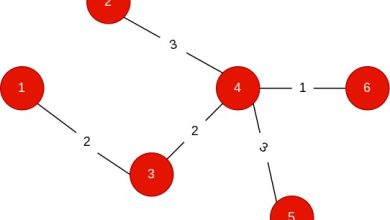
আগের লিখায় আমরা বেলম্যান ফোর্ড অ্যালগরিদম নিয়ে দেখেছিলাম। তারও আগে আমরা বিএফএস অ্যালগরিদম নিয়ে দেখেছিলাম। আমার আজকের লিখাটা হলো ডায়াক্সট্রা অ্যালগরিদম (Dijkstra Algorithm) নিয়ে। এই অ্যালগরিদম, আমাদের আগে দেখা বিএফএস অ্যালগরিদম এরই জাতভাই। তবে বিএফএস অ্যালগরিদম ওয়েটেড গ্রাফে কাজ করে না আর ডায়াক্সট্রা অ্যালগরিদম ওয়েটেড গ্রাফেও কাজ করে। তবে বেলম্যান ফোর্ড অ্যালগরিদমের মতো ডায়াক্সট্রা অ্যালগরিদম (Dijkstra algorithm) গ্রাফে নেগেটিভ সাইকেল (Negative cycle) থাকলে কাজ করে না।
গ্রাফ নিয়ে বেসিক ধারনা পেতে আমার এই লিখাটি পড়তে পারেন গ্রাফ বেসিক: গ্রাফ এবং গ্রাফ এর রিপ্রেজেন্টেশন
ডায়াক্সট্রা অ্যালগরিদম (Dijkstra Algorithm) বাংলা টিউটোরিয়াল
এটা শুরু করার আগে আমি আশা করে নিচ্ছি আপনারা বিএফএস অ্যালগরিদম (BFS Algorithm) নিয়ে একটু দেখেছেন। না দেখলেও এটা দেখে যেতে পারেন, অথবা আমাদের বিএফএস নিয়ে পোস্ট টি দেখেতে পারেন। গ্রাফঃ বিএফএস (BFS) গ্রাফ ট্রাভার্সাল অ্যালগরিদম। ডায়াক্সট্রা অ্যালগরিদম হলো সকল শর্টেস্ট পাথ অ্যালগরিদমের চেয়ে ক্লাসিকাল একটা অ্যালগরিদম।
ধরেন আপনি জানতে চাচ্ছেন মুক্তাগাছা (u) (আমার জন্মস্থান) থেকে ঢাকা (v) যেতে হলে কোন রাস্তাতে (E) গেলে সব থেকে দ্রুত হবে। এখন মুক্তাগাছা থেকে ঢাকা বেশ কয়েকটি রাস্তা দিয়ে যাওয়া যায়। তার মধ্যে সবচেয়ে সংক্ষিপ্ত পথ হলে ময়মনসিংহ হেমায়েতপুর বাইপাস রাস্তা। তো কম্পিউটারে এই ক্ষুদ্রতম রাস্তা বের করার জন্য ডায়াক্সট্রা অ্যালগরিদম আপনাকে সাহায্য করতে পারবে।
এবার কাজে নামা যাক। বেলম্যান ফোর্ডের মতো ডায়াক্সট্রা অ্যালগরিদম সিঙ্গেল সোর্স শর্টেস্ট পাথ অ্যালগরিদম (Single source shortest path)। অর্থাৎ, এই অ্যালগরিদম দিয়ে আপনি নির্দিস্ট কোন নোড থেকে সকল নোডের মধ্যে যেতে সর্বোনিম্ন কস্ট বের করতে পারবেন। আমরা বিএফএস অ্যালগরিদম করার সময় Queue (std::queue<>) ডাটা-স্ট্রাকচার ব্যাবহার করেছিলাম।
আমাদের প্রসেসটা ছিলো নিম্নরূপঃ
- আমাদের সোর্স নোডকে কিউ তে পুশ করেছি।
- যতক্ষণ পর্যন্ত কিউ (Queue) খালি না হয় ততক্ষণ পর্যন্ত আমরা একটি লুপ নিয়েছি এবং প্রতিবারে আমরা কিউয়ের সবার সামনের নোডকে বের করে নিয়েছি।
- তারপর আরেকটা লুপের মধ্যে চেক দিতাম তার একটি এডজাসেন্ট নোড (v) কে কি আগে ভিজিট করা হয়েছে? না করা হলে v কে ভিজিটেড মার্ক করে তাকে কিউতে পুশ করতাম।
- আমাদের এই অ্যালগরিদম ও একই রকমের, শুধু পার্থক্য হলো বিএফএস শুধু আনওয়েটেড গ্রাফে কাজ করে বলে আমাদের ভিজিটেড নোড গুলোকে মার্ক করে দিলেই হতো। কারণ হিসেবে আমরা এই ছবিটি দেখতে পারি।

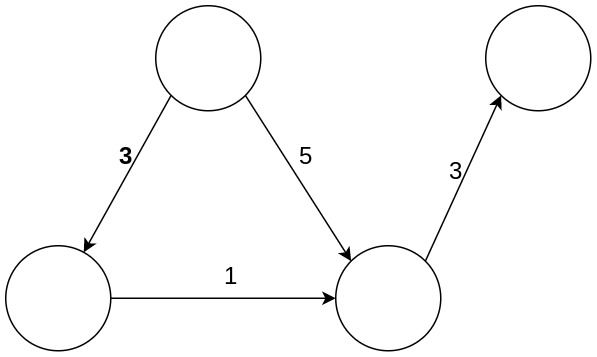
এখানে প্রথম ছবিটি একটি আনওয়েটেড গ্রাফের (Unweighted graph)। দুই নং ছবিটি ওয়েটেড গ্রাফের (Weighted graph)। আমরা দেখছি, আনওয়েটেড গ্রাফের জন্য ১ নং নোড (u) থেকে ৩ নং নোডে (v) গেলেই ১ থেকে ৩ নং নডের শর্টেস্ট পাথ ১ বের করা যায়। তাই বিএফএস অ্যালগরিদম আমাদেরকে ৩ নং নোডে একবার গেলেই হয়। তবে, দুই নং চিত্রে দেখছি প্রথম বারে ১ থেকে ৩ নং নোডে গেলে মিনিমাম কস্ট হিসেবে ৫ আসবে। কিন্তু ১->২->৩ নং নোডে গেলে কস্ট ৩ হবে। তাই ওয়েটেড গ্রাফে এক নোডে একবার গেলেই হবে না। বেশ কয়েকবার যেতে হবে। তাই আমরা বিএফএসের আপডেট অংশ নিচের মতো করে পরিবর্তন করে দিবো।
| 1 2 3 4 5 6 7 | while Queue is not empty: u = Queue.top() Queue.pop() for all v from u: if distance[u]+cost[u][v]<distance[v]: distance[v]=distance[u]+cost[u][v] //এখানে cost[u][v] মানে u নোড থেকে v তে যাওয়ার কস্ট কে বুঝাচ্ছি। Queue.push(v) |
এই কোডে যতক্ষণ পর্যন্ত আপডেট করা যাবে ততোক্ষণ পর্যন্ত আপডেট হতে থাকবে। আমরা চাইলেই প্রায়োরিটি কিউ (Priority Queue) ব্যাবহার করে এই কোডের টাইম কমপ্লেক্সিটি কমাতে পারি। আইডিয়াটি হলো আমরা সোর্স নোডের সবথেকে কাছের নোডকে নিবো। এতে করে এতে করে আমাদের একটি নোডকে অনেক কম সংখ্যক বার আপডেট করা লাগতো।
Dijkstra Algorithm: কেন প্রায়োরিটি কিউ?
priority queue সবসময় সোর্স নোড থেকে পরবর্তী কাছের নোড গুলোর সিলেকশন নিশ্চিত করে। আমরা যদি বিএফএস অ্যালগরিদমের মতো FIFO (First In First Out) টেকনিক প্রয়োগ করতাম তাহলে আমাদের কিউ থেকে আগে আসবে আগে বেরোবেন ভিত্তিতে নোড বের হত। এতে করে দেখা যেতো লেভেল ভিত্তিতে আপডেট করা লাগতো যা priority_queue ব্যাবহার করলে ঘটবে না। প্রায়োরিটি কিউ ব্যাবহার না করলে এই এলগরিদমের রানটাইম দাড়ায় , যেখানে V=নোডের সংখ্যা এবং E=এজের সংখ্যা। অন্য দিকে প্রায়োরিটি কিউ দিয়ে এর কমপ্লেক্সিটি হয়
আমরা কোডটি দেখি এখন, তারপর প্রত্যেকটি লাইন ধরে ব্যাখ্যা করবো।
Dijkstra Algorithm Code in C++
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 | /* Sharif Hasan - CSE, PUST Apr 24, 2020 02: 14 PM */ #include<bits/stdc++.h> using namespace std; struct Node{ Node(int u,int d){ at=u; distance=d; } int at,distance; }; bool operator < (Node A,Node B){ return A.distance>B.distance; } /*Main function*/ int main() { int MAX_NODES=6; int source_node=0; /* এখানে আমাদের adjacency_list তৈরি করা হয়েছে। */ vector <Node> adjacency_list[MAX_NODES]; adjacency_list[0].push_back(Node(1,INT_MAX)); adjacency_list[0].push_back(Node(2,INT_MAX)); adjacency_list[1].push_back(Node(3,INT_MAX)); adjacency_list[1].push_back(Node(4,INT_MAX)); adjacency_list[2].push_back(Node(3,INT_MAX)); adjacency_list[2].push_back(Node(4,INT_MAX)); adjacency_list[3].push_back(Node(4,INT_MAX)); adjacency_list[3].push_back(Node(5,INT_MAX)); adjacency_list[4].push_back(Node(5,INT_MAX)); /* @ নোড u থেকে নোড v তে যাওয়ার জন্য cost[u][v] তে বসিয়ে রাখি। */ int cost[MAX_NODES][MAX_NODES]={-1}; cost[0][1]=10; cost[0][2]=20; cost[1][3]=50; cost[1][4]=10; cost[2][3]=20; cost[2][4]=33; cost[3][4]=20; cost[3][5]=2; cost[4][5]=1; priority_queue <Node> pq; pq.push(Node(source_node,0)); //সোর্স নোডকে priority queue তে পুশ করে রাখি এবং ডিসটেন্স ০ করে রাখি। int saved_distance[MAX_NODES]; for(int i=0;i<MAX_NODES;i++) saved_distance[i]=INT_MAX; saved_distance[0]=0; while(!pq.empty()){ //ততক্ষণ না পর্যন্ত priority queue খালি না হয় Node u=pq.top(); pq.pop(); for(auto v:adjacency_list[u.at]){ /* @ এই লাইন টা আনকমেন্ট করে দেখুন cout<<u.at<<" to "<<v.at<<", prev in v= "<<saved_distance[v.at]<<", new= "<<saved_distance[u.at]+cost[u.at][v.at]<<endl; */ if(saved_distance[v.at]>saved_distance[u.at]+cost[u.at][v.at]){ v.distance=u.distance+cost[u.at][v.at]; saved_distance[v.at]=v.distance; pq.push(v); } } } for(int i=0;i<MAX_NODES;i++){ cout<<"distance from 0 to "<<i<<" is "<<saved_distance[i]<<endl; } return 0; } |
ডায়াক্সট্রা অ্যালগরিদমের কোডের ব্যাখ্যা
উপড়ে আমরা যেই কোডটি দেখতে পাচ্ছি এটিই ডায়াক্সট্রা অ্যালগরিদম এর C++ ইমপ্লিমেন্টেশন। এখানে আমরা C/C++ এর struct ফিচার ব্যাবহার করে নোড তৈরি করেছি যেখানে, নোড নাম্বার (at) এবং সোর্স নোড থেকে দূরত্ব (distance) এই দুইটি ফিল্ড আছে। আমাদেরকে Less then (<) অপারেটর অভেরলোড করা লেগেছে। কারণ এই কোডে আমরা C++ stl priority_queue ব্যাবহার করেছি, যেখানে দুইটি ইলিমেন্টের মধ্যে তুলনা করা লাগে। এই দুইটি কাজ ৮ থেকে ১৮ নং লাইনের মধ্যেই করা হয়েছে।
লাইন ২২ এবং ২৩ এ আমরা দুইটি ভারিয়েবল MAX_NODES এবং source_node নিয়েছি, একটাতে বলেছি আমাদের মোট কয়টি নোড আছে এবং আরেকটাতে বলেছি আমাদের সোর্স নোড কোনটি।
| 22 23 | int MAX_NODES=6; int source_node=0; |
আমরা ৬ টি নোড নিয়ে কাজ করবো তাই MAX_NODES এর মান দিয়েছি 6 এবং আমারদেরকে নোড শূন্য থেকে সকল নোডের দূরত্ব বের করতে হবে তাই সোর্স নোডের মান 0।
লাইন ২৮ থেকে ৪২ এ আমরা আমাদের নিচের গ্রাফকে adjacency list এর মাধ্যমে উপস্থাপন করেছি।
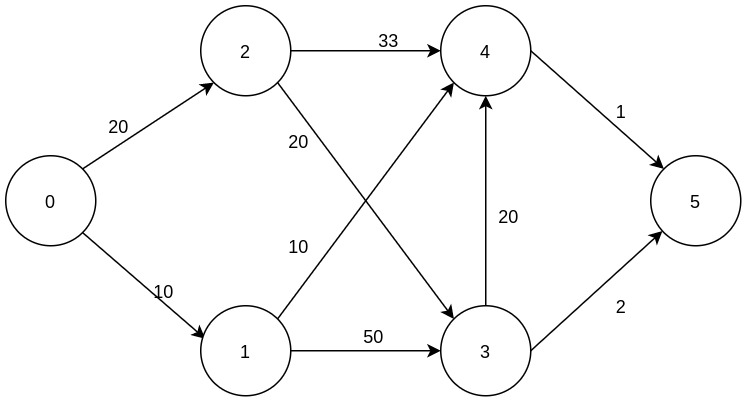
vector <Node> adjacency_list[MAX_NODES]; এই লাইনের মাধ্যমে আমরা std::vector <Node> টাইপের একটি অ্যারে নিয়েছি যার প্রতিটা ইনডেক্স u হলে ঐ vector এর বাকি নোড গুলো গন্তব্য নোড v কে উপস্থাপন করে। এখানে আমরা Node(নোড নাম্বার,নোড ডিসটেঁন্স) দিয়ে প্রতিটা নোড তৈরি করেছি, এবং ভেক্টর এ পুশ করে রেখেছি, এভাবে
| 1 | adjacency_list[u].push_back(Node(v,INT_MAX)); |
এখানে INT_MAX ব্যাবহার করা হয়েছে কারণ প্রথমেই আমরা জানি না ক্ষুদ্রতম পথ কতো, তাই প্রাথমিক ভাবে অনেক বড় একটা মান দেয়া হয়েছে। (Node Structure এর distance ফিল্ড টা শুধু প্রায়োরিটি কিউয়ের জন্য)
এবার আমাদের প্রত্যেকটি এজের (Edge) জন্য কস্টের মান সেট করতে হবে। এর জন্য আমরা একটি 2D array ব্যাবহার করবো cost নামে। এখানে প্রথম ইনডেক্স আমাদের কে দুটি নোডের প্রথম নোড u নির্দেশ করবে, এবং দ্বিতীয় নোড আমাদের গন্তব্য নোড v নির্দেশ করবে। লাইন ৪৭ থেকে ৫৬ নং লাইনের মধ্যে এই কাজ গুলো করা হয়েছে। যেমন ৪৮ নাম্বার লাইনে আমরা 0 থেকে 1 এ যাওয়ার কস্ট 10 সেট করেছি cost[0][1]=10; এই কোডের মাধ্যমে।
৫৮ থেকে ৬০ নং লাইনে আমরা ০ নোড থেকে সকল নোডের দূরত্ব সেভ করে রাখার জন্য saved_distance নামে একটি array নিয়েছি এবং প্রাথমিক ভাবে নোড ০ বাদে বাকি নোড গুলোর দূরত্ব অসীম করে দিয়েছি। একমাত্র নোড ০ এর দূরত্ব ০ করা হয়েছে কারণ ০ থেকে ০ নোডের দূরত্ব শূন্য।
৬২ থেকে ৬৩ নং লাইনে আমরা একটি priority_queue নিয়েছি। যার মধ্যে আমরা Node টাইপ গ্রাফের নোড গুলো রাখব।
| 62 63 | priority_queue <Node> pq; pq.push(Node(source_node,0)); |
৬৩ নং লাইনে আমরা শুন্য নং নোড সোর্স নোড হিসেবে রেখেছি।
লাইন ৬৭ থেকে ৮২ এখানেই আমরা মুল কাজটি করেছি। একটি while লুপ আছে। যতক্ষণ পর্যন্ত priority_queue pq খালি না হয় ততক্ষণ পর্যন্ত ঘুরবে।
| 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 | while(!pq.empty()){ //ততক্ষণ না পর্যন্ত priority queue খালি না হয় Node u=pq.top(); pq.pop(); for(auto v:adjacency_list[u.at]){ /* @ এই লাইন টা আনকমেন্ট করে দেখুন cout<<u.at<<" to "<<v.at<<", prev in v= "<<saved_distance[v.at]<<", new= "<<saved_distance[u.at]+cost[u.at][v.at]<<endl; */ if(saved_distance[v.at]>saved_distance[u.at]+cost[u.at][v.at]){ v.distance=u.distance+cost[u.at][v.at]; saved_distance[v.at]=v.distance; pq.push(v); } } } |
৬৮ নং লাইনে priority_queue এর সবথেকে ছোট distance এর নোড বের করে এনে তা ডিলিট করে দিয়েছি ৬৯ নং লাইনে। তারপর এই নোডের সমস্ত adjacent node কে চেক করে দেখেছি তাদের নোড আপডেট করা যায় নাকি। এখানে চেক করার শর্ত হলো
if( saved_distance[v.at]>saved_distance[u.at]+cost[u.at][v.at] )
এটাকে যদি বাংলায় বলি তাহলে এমন দাড়ায়, যদি আমাদের গন্তব্য নোড (v) তে সোর্স নোড থেকে আগের সেভ করা দূরত্বটি বর্তমান নোডের (u) এর সোর্স থেকে দূরত্ব এবং u থেকে v তে যাওয়ার যেই কস্ট তার যোগফলের চেয়ে বড় হয়, তবে u থেকে v তে যাওয়াই বেস্ট রাস্তা। যদি যদি এর শর্তটি সত্য হয় তবে, ৭৭ এবং ৭৮ নং লাইনে আমরা Node, v কে আপডেট করে নিয়েছি এবং পরে আমরা saved_distance কেউ আপডেট করে দিয়েছি। এবং আপডেটেড নোড v কে আবার priority_queue pq তে পুশ করেছি। (লাইন ৭৯)
এবং সবশেষে ৮৪ থেকে ৮৬ নং লাইনে আমরা আউটপুট দেখতে পাচ্ছি।
| 84 85 86 | for(int i=0;i<MAX_NODES;i++){ cout<<"distance from 0 to "<<i<<" is "<<saved_distance[i]<<endl; } |
নেগেটিভ সাইকেল? সমস্যা কি?
একটি কমন প্রশ্ন হলো গ্রাফে নেগেটিভ সাইকেল থাকলে ডায়াক্সট্রা কেন কাজ করে না? গ্রাফে নেগেটিভ সাইকেল থাকার অর্থ হলো কোন নোড থেকে সাইকেল ঘুরে আবার ঐ নোডে আসলে মোট কস্ট ঋণাত্মক হবে। এখন যদি কোন ঋণাত্মক সাইকেলে পরে যায় আমাদের অ্যালগরিদম তাহলে আমাদের কিউ কখনো খালি হবে না। অর্থাৎ ইনফিনিট লুপে পরে যাবে। নেগেটিভ সাইকেল থাকা মানে আপনি যতখুশি তত কস্ট কমাতে পারবেন। আরও জানতে Bellman Ford Algorithm এই লিখায় দেখুন।
ডায়াক্সট্রা অ্যালগরিদম এনালাইসিস (Dijkstra algorithm analysis)
আমরা যদি এখানে কিউ ব্যাবহার না করতাম তাহলে এখানে যেভাবে বলা আছে এভাবে আমাদের Time complexity দাঁড়াত । তবে আমরা যেহেতু প্রায়োরিটি কিউ ব্যাবহার করেছি তাই আমাদের কমপ্লেক্সিটি হচ্ছে । কারণ প্রায়োরিটি কিউ তে প্রতিবার সর্ট করতে সময় লাগবে।
আজকে এই পর্যন্তই। আজকের লিখাটা আমার পারফেক্ট মনে হচ্ছে না। কিন্তু অর্ধেক লিখে ফেলছিলাম, তাই সম্পুর্ন করলাম। আপনাদের কেমন লাগলো কমেন্ট করতে ভুলবেন না। ভুল ক্রুটি হলে আমার ফেসবুক/ মেইল বা কমেন্ট বক্সে জানানোর জন্য অনুরোধ করছি। #happy_coding