টারনারি সার্চ (Ternary search) অ্যালগরিদম হলো এমন একটি সার্চ অ্যালগরিদম যেখানে আমরা আমাদের সার্চ রেঞ্জকে (যেই রেঞ্জে আমরা সার্চ করি তাই সার্চ রেঞ্জ) তিনভাগে ভাগ করে সার্চ করে। আমরা আগের লিখা, বাইনারি সার্চে দেখেছিলাম আমরা আমাদের রেঞ্জকে দুই ভাগে ভাগ করেছি। একটি ভাগ এর বামে, আরেকটি ডানে।
তবে টারনারি সার্চের ক্ষেত্রে আমরা আমাদের সার্চ রেঞ্জে (বা অ্যারের যেটুকুতে আমরা আছি) দুইটি পয়েন্ট নিবো। একটি এবং আরেকটি । এবং দ্বারা আমাদের অ্যারে তিন ভাগে ভাগ হবে, প্রথম অংশ হবে সর্বনিম্ন রেঞ্জ বা থেকে পর্যন্ত। তারপর দ্বিতীয় অংশ থেকে এবং তৃতীয় অংশ হবে থেকে সর্ব ডানের রেঞ্জ বা
Ternary search Bangla Tutorial
টারনারি সার্চ একটি ভাগ কর শাসন করো বা Divide and conquer অ্যালগরিদম। বাইনারি সার্চের থেকে এর খুব বেশি একটা তফাত নেই। তাই এটা পড়ার আগে বাইনারি সার্চ নিয়ে জানা থাকলে সুবিধা পাবেন।
বাইনারি সার্চের মতো টারনারি সার্চ অ্যালগরিদমে কাজ করতে হলে আমাদের সর্টেড অ্যারে দরকার হয়। ধরা যাক আমাদের সাইজের কোনও অ্যারে থেকে একটি সংখ্যা কে খুঁজে বের করতে হবে। আমরা প্রতিবার নিচের মতো করে স্টেপ নিবো,
টারনারি সার্চ অ্যালগরিদম (Ternary search algorithm)
- অ্যারেটাকে সর্ট করে নিই।
- প্রথমে এবং [ শুন্য ভিত্তিক ইন্ডেক্সিং ]
- যতক্ষণ হয় ততক্ষণ আমরা …
- এবং বের করি নিচের সূত্র মতো।
- এর সাথে আমরা কে তুলনা করি। যদি আমাদের এর সমান হয় তবে true রিটার্ন করি। নয়তো পরের ধাপে যাই।
- এর সাথে আমরা কে তুলনা করি। যদি আমাদের এর সমান হয় তবে true রিটার্ন করি। না হলে পরের ধাপে যাই।
- যদি এর মান এর থেকে ছোট হয় তাহলে আমরা বামে যাবো। ( সেট করতে হবে)
- অথবা যদি এর মান এর থেকে বড় হয় তবে ডানে যাবো। ( সেট করতে হবে)
- নয়তো আমরা নিশ্চিত যে কে আমরা থেকে এই রেঞ্জেই খুঁজে পাবো। তাই আমরা মাঝেই থাকবো। ( এবং ) সেট করতে হবে)
- পুনরায় ৩ নং এ যাই।
- এবং বের করি নিচের সূত্র মতো।
আমরা দেখতে পাচ্ছি টারনারি সার্চ অ্যালগরিদমটি বাইনারি সার্চের মতোই সজাসাপ্টা একটি অ্যালগরিদম। এই অ্যালগরিদমটিকেও আমরা বাইনারি সার্চের মতো খুব সহজেই ইমপ্লিমেন্ট করতে পারি। রিকার্শন অথবা লুপের মাধ্যমে খুব সহজেই এর কোড করা যাবে।
টারনারি সার্চ কিভাবে কাজ করে?
আমরা এখন টারনারি সার্চ কিভাবে কাজ করে তার একটি কমপ্লিট ভিজুয়ালাইজেশন দেখবো। ধরা যাক একটি অ্যারেতে আমদের একটি সংখ্যা খুঁজতে বলা হয়েছে। আমরা নিচের মতো করে অগ্রসর হবো।

আমরা একটি অ্যারে নিবো যেখানে এলিমেন্ট হিসেবে ১,৪,৭,৯,২০,২২,৩৩,২৪,৪৫,৪৭ এই গুলো রাখা আছে এবং যার সাইজ n=10। আমরা অ্যারেটিকে আগেই সর্ট করে নিয়েছি। তারপর আমরা পরের ধাপে যাবো।

এখানে আমরা দেখতে পাচ্ছি l=0 এবং r=9, যা আমাদের শর্ত পূরণ করে। তাই আমরা সূত্র মোতাবেক এবং এর মান বের করবো।
এখানে কনটাই আমাদের টার্গেট x=22 এর সমান নয়।
যেহেতু x=22 , ৯ থেকে বড় এবং ৩৩ থেকে ছোট তাই আমাদের পরবর্তী সার্চ রেঞ্জ হবে এবং .
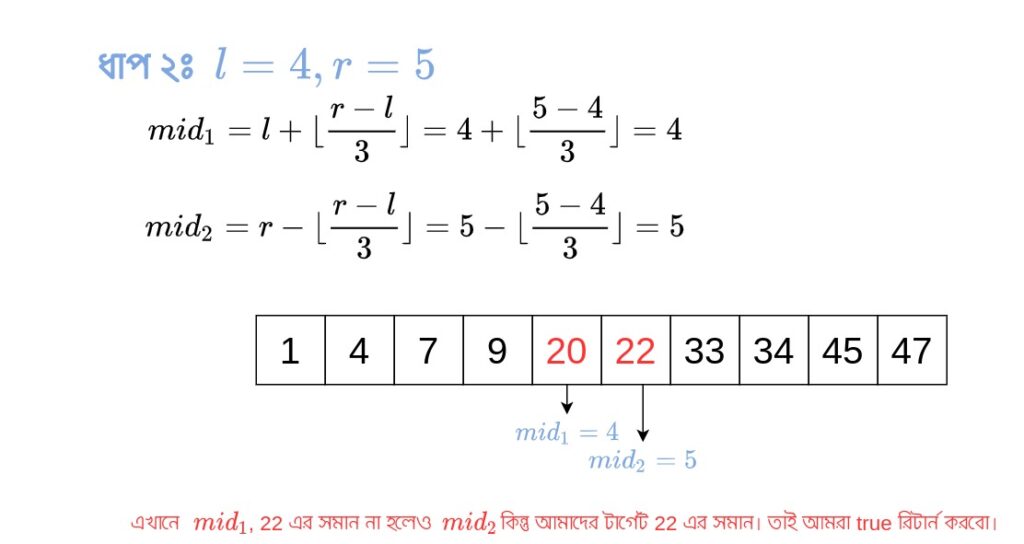
এই ধাপটিও আমাদের শর্ত পূরণ করে। তাই, আমরা ১ নং ধাপের মতো করে এবং এর মান হিসেব করবো। তারপর আমরা দেখবো অ্যারের এই দুটি পয়েন্টে কি আমাদের টার্গেট এলিমেন্ট আছে কি না। যেহেতু আছে (), তাই আমরা true রিটার্ন করেছি।
টারনারি সার্চ ইমপ্লিমেন্টেশন (Ternary search implementation) [C++]
টারনারি সার্চ ইমপ্লিমেন্ট করাও বাইনারি সার্চের মতোই সহজ, তাই আমরা আগের পোস্টের বাইনারি সার্চের কোডটাকেই একটু মডিফাই করছি।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | #include <bits/stdc++.h> using namespace std; int main(){ int n=9; int arr[n] ={5,3,4,7,8,2,1,8,9}; sort(arr,arr+n); int l=0,r=n-1; int target=5; while(l<=r){ int mid1=l+(r-l)/3; int mid2=r-(r-l)/3; if(arr[mid1]==target||arr[mid2]==target){ cout<<target<<" found\n"; return 0; }else if(target<arr[mid1]){ r=mid1-1; //go left }else if(target>arr[mid2]){ l=mid2+1; //go right }else{ /* go middle */ l=mid1+1; r=mid2-1; } } cout<<target<<" not found\n"; return 0; } |
এখানে ১৫ নং লাইনে চেক করেছি অথবা এই দুটি পয়েন্টের কনটাতে আমাদের target আছে কিনা। যদি থাকে তাহলে এখানেই প্রিন্ট করে দিয়েছি।
নয়তো আমরা টার্গেটের উপর এবং এর উপর ভিত্তি করে সিদ্ধান্ত নিয়েছি কোন দিকে যাবো। যেহেতু আমাদের অ্যারেটা সর্টেড অ্যারে, তাই টার্গেট যদি এর এলিমেন্ট থেকে কম হয় তাহলে আমরা বামে যাবো। তাই সেট করে দিয়েছি। যদি টার্গেট এর এলিমেন্ট থেকে বড় হয় তবে আমরা তিন নম্বর অংশ বা ডানে যাবো। তাই সেট করে দিয়েছি। নয়তো আমরা নিশ্চিত যে আমাদের এলিমেন্ট থেকে এর রেঞ্জে রয়েছে। তাই এক্ষেত্রে আমরা সেট করে দিয়েছি। অতবার পুনরায় লুপ চালিয়েছি।
টারনারি সার্চ অ্যালগরিদম এনালাইসিস
যেহেতু টারনারি সার্চ প্রতিবার আমাদের অ্যারেকে তিন ভাগে ভাগ করছে। তাই আমাদের সার্চের টাইম কমপ্লেক্সিটি হলো ।
বাইনারি সার্চ বনাম টারনারি সার্চ
প্রথমেই টারনারি সার্চ বাইনারি সার্চের চেয়ে আস্তে চলে। আপাত দৃষ্টি তে টারনারি সার্চকে দ্রুত মনে হলেও বাস্তবে বাইনারি সার্চ বেশি দ্রুত। বাইনারি সার্চের বাজে কেসে সার্চ কমপ্লেক্সিটি । অপর দিলে টারনারি সার্চের সার্চ কমপ্লেক্সিটি । সুতরাং দেখা যাচ্ছে বাইনারি সার্চ, টারনারি সার্চ থেকে দ্রুত।
টারনারি সার্চ প্র্যাকটিস প্রবলেম:
- https://www.codechef.com/problems/AMCS03
- http://codeforces.com/problemset/problem/578/C
- http://lightoj.com/volume_showproblem.php?problem=1146
- https://codeforces.com/contest/439/problem/D
টারনারি সার্চের এবং বাইনারি সার্চের কিছু আলাদা আলাদা আপ্লিকেশন আছে। আমরা পরবর্তি কোন লিখাতে আলোচনা করবো ইনশাল্লাহ। #Happy_Coding
আরও পরুন: বাইনারি হিপ (Binary Heap) বা প্রায়োরিটি কিউ (Priority Queue)