Data structure নিয়ে আগের লিখায় বাইনারি সার্চ ট্রি নিয়ে জেনেছিলাম। ঐখানে আমরা দেখেছিলাম কিভাবে বাইনারি সার্চ ট্রি (BST) ব্যবহার করে ইনপুট গুলো সর্টেড (Sorted) অর্ডার এ রাখতে পারি এবং দরকার মতো তা এভারেজ কেস এ O(log n) এ বের করতে পারি। আমরা সেখানে BST এর একটি সীমাবদ্ধতা দেখেছি, Binary Search Tree (BST) তে সর্টেড নাম্বার ইনপুট দিলেই বাজে কেস (Worst case) তৈরি হয় এবং তখন O(n) এ সার্চ, ডিলিট এবং ইনসার্ট অপারেশন করতে হয়। এই সমস্যা সমাধানের জন্যই আমাদেরকে বাইনারি সার্চ ট্রি ব্যালেন্স করে রাখতে হয়। Balanced Binary Search Tree এর জন্য বেশ কিছু ডাটা স্ট্রাকচার রয়েছে। যেমন AVL ট্রি, রেড ব্ল্যাক ট্রি (Red Black Tree), ট্রিপ (Treap) ।
এই লেখাটি অনেক বড় হতে চলেছে। AVL Tree এর লজিক বুঝানো আমার মনে হলো একটু কঠিনই। তবুও আমি আমার সাধ্যমত চেষ্টা করেছি। আপনারা এই লিখাটি ধাপে ধাপে পরুন। যেমন প্রথমে উচ্চতা (Height) বের করার লজিক দেখুন। তারপর ঘূর্ণনের (Rotation) লজিক। সবার শেষে ইমপ্লিমেন্টেশন (Implementation) বুঝুন। কাজ হবে ইনশাল্লাহ।
AVL Tree Bangla Tutorial
এই লিখাটি পড়ার আগে আপনার ট্রি (Tree) নিয়ে বেসিক ধারনা থাকতে হবে, বাইনারি সার্চ ট্রি কি তা বুঝতে হবে এবং রিকার্শনের (Recursion) বেসিক বুঝতে হবে।
আজকে আমার লিখাটা AVL Tree নিয়ে। AVL Tree হলো সেলফ বেলেন্সিং বাইনারি সার্চ ট্রি (Self Balancing Binary Search Tree)। AVL Tree তে আমরা যখন সংখ্যা রাখবো তখন কোন কারণে বাইনারি সার্চ ট্রি এর ভারসাম্য নষ্ট হলে AVL Tree অ্যালগরিদম নিজে নিজে Tree এর ভারসাম্য তৈরি করে নিতে পারবে। এভিএল ট্রি (AVL Tree) এর নামকরণ হয়েছে তাদের আবিষ্কারকদের (Adelson, Velski , Landis) নাম অনুসারে।
AVL Tree বাইনারি সার্চ ট্রি বা BST এর সকল বৈশিষ্ট্য ধারণ করে। এর মধ্যে যে বিশিষ্টের জন্য AVL Tree অনন্য তা হলো এই ট্রি সবসময় ব্যালেন্স থাকে। যার জন্য ট্রি এর উচ্চতা বা সর্বোচ্চ লেভেল O(log n) এর সীমাবদ্ধ রাখা যায়। ফলে আমাদের ট্রি এর বাজে কেসে কমপ্লেক্সিটি O(n) থেকে O(log n) এ উন্নতি হয়। কারণ আমরা জানি বাইনারি সার্চ ট্রি তে বাজে কেস কমপ্লেক্সিটি ট্রি এর উচ্চতার উপর নির্ভর করে।
ব্যালান্সড বাইনারি ট্রি কি – What is balanced binary tree?

ব্যালান্সড বাইনারি ট্রি হলো এমন একটি ডেটা স্ট্রাকচার (Data structure) যেখানে ট্রি এর বাম এবং ডান সাবট্রির উচ্চতার সর্বোচ্চ পার্থক্য ১ হয়। চিত্রে একটি ভারসাম্যহীন (Imbalanced) বাইনারি ট্রি আরেকটি ভারসাম্যে (Balanced) থাকা বাইনারি ট্রি দেখানো হয়েছে। ডানের চিত্রের জন্য সকল সাব-ট্রির বাম সাব-ট্রি থেকে ডান সাব-ট্রির সর্বোচ্চ উচ্চতার পার্থক্য সর্বোচ্চ ১ (প্রকৃতপক্ষে শুন্য) এর মধ্যে আছে। অন্য দিকে বামের ট্রি তে রুট নোডের বাম সাব-ট্রি খালি, কিন্তু ডান সাবট্রির উচ্চতা ৭, তাই এটা ব্যালান্সড বাইনারি ট্রি নয়।
AVL ট্রি নিয়ে জানার আগে আমাদের দুইটি বিষয় ভালো করে শিখে নিতে হবে। এদের মধ্যে একটি হলো (১) ইনসার্ট এর সময় বাইনারি সার্চ ট্রি এর উচ্চতা বের করা O(log n) সময়ে, এবং (২) বাইনারি সার্চ ট্রিয়ের যেকোনো তিনটি নোড কে বামে, ডানে ঘোরানো। এই দুইটি বিষয় কাজে লাগিয়ে AVL ট্রিকে ব্যাল্যান্স করে রাখা হয়।
AVL Tree Bangla tutorial – Part 1
ইনসার্টের সময় AVL বাইনারি সার্চ ট্রিয়ের (BST) উচ্চতা বের করা
যেহেতু AVL ট্রি একধরনের বাইনারি সার্চ ট্রি তাই আমাদের AVL ট্রি তে ইনসার্ট এর প্রক্রিয়া প্রায় বাইনারি সার্চ ট্রি এর মতোই এবং আমাদেরকে বাইনারি সার্চ ট্রি এর সমস্ত বৈশিষ্ট্য অক্ষুণ্ণ রেখে ইনসার্ট করতে হয়। আমরা আগের লিখাটা থেকে বাইনারি সার্চ ট্রি এর ইনসার্ট এর কোডটুকু একটু পরিবর্তন এর মাধ্যমে উচ্চতা (Height) বের করার প্রোগ্রাম করেছি।

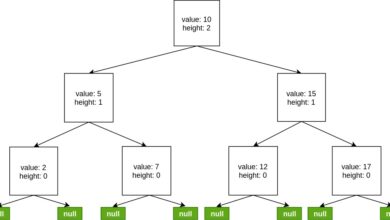
আমরা প্রথমে ট্রি এর উচ্চতার সংজ্ঞা দেখি, বাইনারি ট্রি এ কোন নোড এর উচ্চতা হলো ঐ নোড থেকে সর্বাধিক দূরত্বের নোডে যেতে যতগুলো এজ (Edge) লাগে তার সংখ্যা। উপরের ২ নং চিত্রে দেখছি নোড ২ এর উচ্চতা দুই, কারণ নোড ২ এর সাবট্রির মধ্যে নোড ৮ সবথেকে বেশি দূরত্বে আছে এবং সেখানে যেতে ২ টি এজ (Edge) পার হতে হয়। একই ভাবে রুট নোড ১ এর উচ্চতা দ্বিতীয় চিত্রে ৩ কারণ, নোড ১ এর সাবট্রির সকল নোডের মধ্যে ৮ সব থেকে দুরে এবং নোড ১ হতে সেখানে যেতে ৩ টি এজ লাগবে।
অর্থাৎ, কোন নোডের উচ্চতা তার বাম এবং ডান নোডের মধ্যে সর্বোচ্চ উচ্চতা যার তার থেকে ১ বেশি। ( এগুলো হলো যথাক্রমে 1,2,3 নং নোডের উচ্চতা। )
আমরা ধরে নিই লিফ নোড বা সবার শেষ লেভেলের নোড গুলোর উচ্চতা শুন্য। আমরা দেখতে পাচ্ছি প্রথম চিত্রে শেষ লেভেলের সবার উচ্চতা ০, এর থেকে উপরের নোডগুলোর উচ্চতা node->height=max(node->left->height,node->right->height)+1 এই সূত্র দিয়ে বের করা যাবে। ১ নং নোডের উচ্চতা হলো ৩ যেহেতু এর বাম সাব-ট্রির উচ্চতা ২ ও ডান সাব-ট্রির সর্বোচ্চ উচ্চতা ১, তাই node->height=max(2,1)+1=3। মনে রাখা লাগবে যে আমরা null নোডের উচ্চতা -1 ধরবো।
AVL Tree code insert() এর ব্যাখ্যা
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | struct Node{ int value; // এখানে ভ্যালু রাখা হবে Node *left_node=NULL; // বামের নোড রাখা হবে এখানে Node *right_node=NULL; // ডানের নোড রাখা হবে এখানে int height=0; //আমাদের ট্রি এর উচ্চতা এখানে জমা রাখা হবে }; int height(Node *node){ if(node==NULL){ return -1; }else{ return node->height; } } Node *insert(int num,Node *node){ if(node==NULL){ //if node==null হলে আমরা বুঝতে পারবো আমরা বাম, ডান করতে করতে সবার শেষে পৌঁছেছি। রুট নোডের ক্ষেত্রেও এই শর্ত সত্য Node *temp=new Node(); // নতুন একটা নোড তৈরি করি temp->value=num; temp->height=0; return temp; }else if(num<=node->value){ //আমরা বামে যাবো, কারণ আমাদের num এর মান বর্তমান নোডের থেকে কম node->left_node=insert(num,node->left_node); }else{ //আমরা ডানে যাবো, কারণ আমাদের num এর মান বর্তমান নোডের থেকে বেশি node->right_node=insert(num,node->right_node); } //বর্তমান নোড (node) এর ডান এবং বাম সাব-ট্রি এর মধ্যে যার উচ্চতা সব থেকে বেশি, আমাদের বর্তমান নোডের উচ্চতা হবে তার থেকে ১ বেশি। node->height=max(height(node->left_node),height(node->right_node))+1; return node; } |
উপরের কোড টুকু সম্পূর্ণ নয়। উপরের কোডটুকুতে আমরা নোডের উচ্চতা বের করার প্রোগ্রাম করেছি।
আমাদের Node struct এ একটু পরিবর্তন করে আমরা int height নামে একটা ফিল্ড তৈরি করেছি। left_node, right_node, value এই ফিল্ডগুলো বাইনারি সার্চ ট্রিয়ের অ্যালগরিদমেই দেখেছিলাম। এই height ফিল্ডে আমরা কোন নোডের উচ্চতাকে আপডেট করে রাখবো।
এখানের সব কিছুই বাইনারি সার্চ ট্রিয়ের নিয়ম অনুযায়ী হয়েছে। আমাদের ইনসার্ট ফাংশনের প্রটোটাইপ হলো, Node *insert(int num, Node *node);
এই ফাংশনটিকে আমরা একটি সংখ্যা (int num) এবং root node এর পয়েন্টার (Node *node) দিয়ে কল করবো এবং এই ফাংশনটি একটি Node type পয়েন্টার (Pointer) রিটার্ন করবে। এই রিটার্ন নোডটি হলো আমাদের ট্রি এর বর্তমান রুট নোড এর এড্রেস। insert() ফাংশনটি একটি রিকার্সিভ ফাংশন। আমরা AVL বাইনারি সার্চ ট্রি এর সাবট্রি গুলোতে রিকার্সনের মাধ্যমে ট্রাভার্স করবো।
| 17 18 19 20 21 22 | if(node==NULL){ //if node==null হলে আমরা বুঝতে পারবো আমরা বাম, ডান করতে করতে সবার শেষে পৌঁছেছি। রুট নোডের ক্ষেত্রেও এই শর্ত সত্য Node *temp=new Node(); // নতুন একটা নোড তৈরি করি temp->value=num; temp->height=0; return temp; } |
insert ফাংশনের ১৭ নং লাইনে আমরা আমাদের রিকার্শনের বেস কেস লিখেছি। কারণ নোড যদি নাল (NULL) হয় তবে আমরা বলতে পারি যে আমরা বাইনারি সার্চ ট্রি এর লজিক অনুসারে এজ বেয়ে বেয়ে একেবারে সবার শেষে পৌঁছেছি। এখানে আমরা নতুন লিফ নোড তৈরি করে নিবো।
এই নোডের value field (১৯ নং লাইন) এ আমরা যেই সংখ্যাটি ইনসার্ট করতে চেয়েছি (num) তা রাখবো। ২০ নং লাইনে আমরা height ফিল্ডে 0 বসাবো। কারণ আমরা জানি লিফ নোডের উচ্চতা শুন্য এবং আমরা নতুন সংখ্যাটির জন্য একটি লিফ নোড তৈরি করেছি। তারপর আমরা নতুন নোডের এড্রেসকে রিটার্ন করে দিয়েছি।
| 22 23 24 25 26 27 28 | else if(num<=node->value){ //আমরা বামে যাবো, কারণ আমাদের num এর মান বর্তমান নোডের থেকে কম node->left_node=insert(num,node->left_node); }else{ //আমরা ডানে যাবো, কারণ আমাদের num এর মান বর্তমান নোডের থেকে বেশি node->right_node=insert(num,node->right_node); } |
২২ থেকে ২৭ নং লাইন গুলোতে আমরা বাইনারি সার্চ ট্রি এর নিয়ম অনুযায়ী ডানে অথবা বামের সাবট্রি তে ইনসার্ট ফাংশন কল করেছি। এবং ইনসার্ট ফাংশন যেই নোডের এড্রেস রিটার্ন করেছিলো তা left_node এবং right_node এ এসাইন করেছি। লক্ষণীয় আমরা এখানেই কিছু রিটার্ন করি নি।
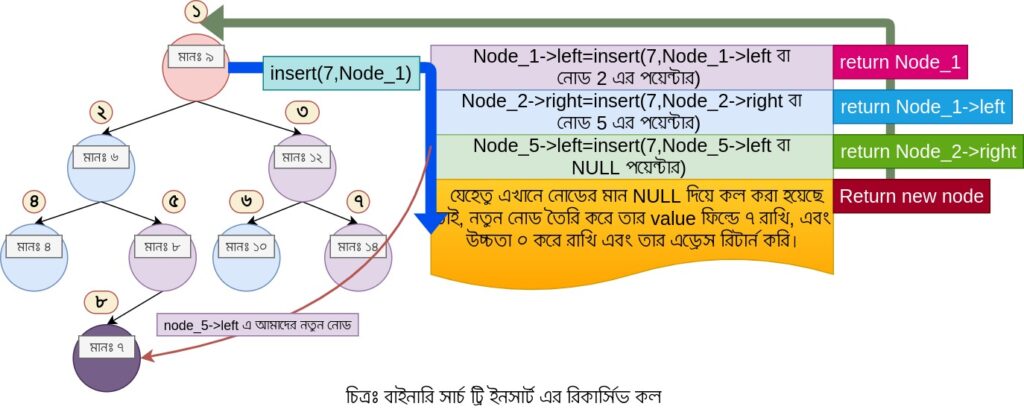
উপরের চিত্রে বাইনারি সার্চ ট্রি তে রিকার্শনের মাধ্যমে 7 কে insert করা হয়েছে। এখানে আমরা দেখতে পারছি, নীল তীর চিহ্ন ধরে আমাদের রিকার্সিভ কল হয়েছে এবং সবুজ তীর চিহ্ন ধরে আমাদের রিটার্ন হয়েছে। আশা করি আপনারা এই প্রসেস টা বাইনারি সার্চ ট্রি পড়ার সময় বুঝেছেন।
এখন ৩১ নং লাইন বা উচ্চতা নির্ণয়ের লাইনে আসি,
| 31 | node->height=max(height(node->left_node),height(node->right_node))+1; |
এইখানে আমরা বর্তমান নোডের height, ডানের সাব-ট্রি এবং বামের সাব-ট্রির মধ্যে সব থেকে বেশি উচ্চতার সাবট্রি এর উচ্চতা নিয়ে তার সাথে ১ যোগ করে সেট করেছি।
আমাদের height ফাংশনটা নিম্নরূপ
| 8 9 10 11 12 13 14 | int height(Node *node){ if(node==NULL){ return -1; }else{ return node->height; } } |
যদি নোডের (Node *node) মান null হয় বা খালি নোড হয় তবে আমাদের height function -1 রিটার্ন করবো। অন্যথায় height function ঐ নোডের উচ্চতা রিটার্ন করবো।
এই গেলো আমাদের নোডের height বের করার কাজ। এখন আমরা AVL ট্রি এর ঘূর্ণন বা Rotation নিয়ে আলোচনা করবো। আপনারা এই কোডটি সিমুলেট করুন খাতায় এবং কোডটি করার চেষ্টা করুন।
AVL Tree Bangla tutorial – Part 2
AVL Tree Rotation
AVL Tree কে ব্যাল্যান্স করার জন্য আমাদের ট্রিয়ের ভিতরে যেকোনো তিনটি নোডকে ঘুরানোর (Rotation) দরকার লাগতে পারে। আমরা প্রথমে আমরা দেখবো AVL ট্রি তে ব্যাল্যান্স ফ্যাক্টর (Balance factor/ bf) কি। তারপর এই ঘূর্ণন কিভাবে করা লাগে তা দেখবো । তারপর দেখবো আমরা insert() function এর ভিতরে কিভাবে Rotation কে ইমপ্লিমেন্ট করা যাবে।
ব্যাল্যান্স ফ্যাক্টর: AVL ট্রি তে ব্যাল্যান্স ফ্যাক্টর হলো ট্রি এর বাম সাবট্রি এবং ডান সাবট্রির উচ্চতার পার্থক্য। সুতরাং ব্যাল্যান্স ফ্যাক্টর বের করার শর্ত হলো,
| 1 | bf=height(node->left_node)-height(node->right_node) |
ব্যাল্যান্স ফ্যাক্টর বা bf (Boy friend ভাবা নিষেধ 😉 ) আমাদের AVL ট্রি কি ব্যাল্যান্স আছে কিনা তা নির্দেশ করে। যদি হয় তাহলেই আমরা বলতে পারবো আমাদের ট্রি ব্যাল্যান্সড রয়েছে। অন্যথায় আমাদের ট্রিকে ঘূর্ণনের মাধ্যমে ব্যাল্যান্স করে নিতে হবে।
AVL Tree তে ঘূর্ণনের প্রকারভেদ
AVL ট্রি তে ৪ ধরনের ঘুর্নন করা যায়। যেমন,
- বামে ঘূর্ণন (Left rotation)
- ডানে ঘূর্ণন (Right rotation)
- বামে-ডানে ঘূর্ণন (Left-Right rotation)
- ডানে-বামে ঘূর্ণন (Right-Left rotation)
বামে ঘূর্ণন বা Left rotation

যদি ৩টি নোডের ডানে নোড থাকার ফলে এমন অবস্থার তৈরি হয় যেখানে কোন নোডের হয়ে যায় তখন এই ধরনের ঘূর্ণন করার মাধ্যমে ট্রি তে ভারসাম্য তৈরি করা লাগে। এই ঘূর্ণন প্রক্রিয়ায় যেই নোডটি ৩ টি নোডের মাঝে আছে (২নং নোড) সেই নোডটিকে রুট নোড করা লাগবে। পূর্বের রুট নোড (১ নং নোড) নোডটিকে মাঝের নোডের বাম নোড হিসেবে এসাইন বা যুক্ত করে দিতে হবে। এবং, যদি ২ নং নোডের কোনও বাম সাবট্রি থাকে তাহলে আমাদেরকে ১ নং নোডের ডান সাবট্রি হিসেবে যুক্ত করতে হবে, এতে করে আমাদের AVL tree তে BST এর সকল বৈশিষ্ট্য সংরক্ষণ হবে।
| 1 2 3 4 5 6 7 8 9 10 11 | Node *left_rotate(Node *node){ Node *temp=node; node=temp->right_node; temp->right_node=node->left_node; // নোড ২ এর বাম সাবট্রি কে নোড ১ এর ডান সাবট্রি হিসেবে দিলাম temp->height=max(height(temp->left_node),height(temp->right_node))+1; //পুনরায় ১ নং নোডের উচ্চতা সেট করতে হবে node->left_node=temp; //২ নং নোডের বাম সাব-ট্রি হিসেবে temp ট্রি টি যুক্ত করি node->height=max(height(node->left_node),height(node->right_node))+1; //পুনরায় ২নং নোডের উচ্চতা হিসাব করি। return node; } |
২ নং লাইনে আমরা বর্তমান নোড (চিত্রে ১ নং নোড) কে সাময়িক ভাবে সর্বক্ষণ করেছি। তারপর ৩ নং লাইনে আমরা ১ নং লাইনের যে ডান নোড আছে (চিত্রের ২ নং নোড) তাকে রুট নোড হিসেবে ধরে নিয়েছি।
যেহেতু, node এখন আমাদের রুট নোড এবং পূর্বের রুট নোড আমরা temp ভারিয়েবলে রেখেছি, তাই আমরা ২ নং নোডের কোন বাম সাবট্রি থাকলে তাকে প্রথমেই ১ নং নোডের ডান সাবট্রি হিসেবে রেখে দিয়েছি ৫ নং লাইনে। তারপর আমরা উচ্চতা বের করার সূত্র অনুসারে ১নং নোডের উচ্চতা বের করেছি ৬ নং লাইনে।
অতঃপর ৮ নং লাইনে আমরা ২ নং নোডের বাম সাব ট্রি হিসেবে ১ নং নোড (temp) কে বসিয়ে দিয়েছি, এবং পরবর্তি লাইনে তার উচ্চতা হিসেব করেছি। সব শেষে আমরা আপডেটেড রুট (node) রিটার্ন করেছি।
ডানে ঘূর্ণন বা Right rotation

যদি ৩টি নোডের বামে নোড থাকার ফলে এমন অবস্থার তৈরি হয় যেখানে কোন নোডের হয়ে যায় তখন এই ধরনের ঘূর্ণন করার মাধ্যমে ট্রি তে ভারসাম্য তৈরি করা লাগে। এই ঘূর্ণন প্রক্রিয়ায় যেই নোডটি ৩ টি নোডের মাঝে আছে (২নং নোড) সেই নোডটিকে রুট নোড করা লাগবে। পূর্বের রুট নোড (১ নং নোড) নোডটিকে মাঝের নোডের ডান নোড হিসেবে এসাইন বা যুক্ত করে দিতে হবে। এবং, যদি ২ নং নোডের কোনও ডান সাবট্রি থাকে তাহলে আমাদেরকে ১ নং নোডের বাম সাবট্রি হিসেবে যুক্ত করতে হবে।
| 1 2 3 4 5 6 7 8 9 10 11 | Node *right_rotate(Node *node){ Node *temp=node; node=temp->left_node; temp->left_node=node->right_node; // নোড ২ এর ডান সাবট্রি কে নোড ১ এর বাম সাবট্রি হিসেবে দিলাম temp->height=max(height(temp->left_node),height(temp->right_node))+1; //পুনরায় ১ নং নোডের উচ্চতা সেট করতে হবে node->right_node=temp; //২ নং নোডের বাম সাব-ট্রি হিসেবে temp ট্রি টি যুক্ত করি node->height=max(height(node->left_node),height(node->right_node))+1; //পুনরায় ২ নং নোডের উচ্চতা হিসাব করি। return node; } |
উপরের কোডটিও বাম ঘূর্ণনের কোডের মতো হওয়ায় ব্যাখ্যা করছি না। না বুঝতে পারলে কমেন্ট করবেন আশা করি।
প্রথমে বামে তারপর ডানে ঘূর্ণন (Left-Right Rotation)
আমরা bf বের করার সূত্র থেকে বলতে পারি যদি bf এর মান ধনাত্মক হয় তবে আমাদের ট্রি এর বাম দিকের সাব ট্রির উচ্চতা বেশি। এই ক্ষেত্রে () আমরা দুইধরনের ঘূর্ণন সম্পন্ন করি। একটি হলো ডানে ঘুরানোর মাধ্যমে ব্যাল্যান্স করা, যা একেবারে সরল রেখা বরাবর নোড গুলো থাকলে প্রয়োগ করা হয়। আরেক ধরনের ঘূর্ণন হলো প্রথমে বামে তারপর ডানে ঘূর্ণন।

যদি কোন নোডে এই ধরনের ভারসাম্যহীনতা তৈরি হয় তবে আমরা লেফট রাইট বা বাম ডান ঘূর্ণন সম্পন্ন করবো। উপরের চিত্রে আমরা নোড ২ কে কেন্দ্র করে প্রথমে বামে ঘূর্ণন করেছি। এতে করে নোড ৩ নোড ২ এর জায়গায় চলে এসেছে এবং নোড ২, নোড ৩ এর বাম নোড হিসেবে চলে গিয়েছে।

এখন যেহেতু নোড ৩ নোড ২ এর জায়গা নিয়েছে এবং নোড ৩ এর লেফট সাব ট্রিতে নোড ২ কে রাখা হয়েছে তাহলে অবশ্যই আমাদেরকে নোড ৩ এর লেফট সাব ট্রি ( যদি থাকে ) তার ব্যাবস্থা করতে হবে। যেহেতু নোড ২ এর রাইট নোডে নোড ৩ ছিলো এবং নোড ২ জায়গা পরিবর্তন করায় নোড ২ এর রাইট সাবট্রি খালি হয়ে পরেছে, তাই আমরা নোড ৩ এর লেফট সাবট্রি কে নোড ২ এর রাইট সাবট্রি হিসেবে আসাইন করে দিবো। এই কাজ গুলো করার পড় আমরা figure 3 এর মতো একটি ট্রি পাবো। এরপর যদি আমরা নোড ১ কে কেন্দ্র করে ডানে ঘুরাই তাহলেই হলো। এই ধাপ শেষ আমাদেরকে নোড ২ এবং ৩ এর উচ্চতা আপডেট করতে হবে।
এর ফলে আমরা figure ৩ নং এর মতো একটি গঠন পাবো। এবার আমরা যদি ডানে ঘূর্ণনের নিয়ম অনুযায়ী ডানে ঘুরাই তবে আমাদের সমস্যা সমাধান হয়ে যাবে। বামে যেই এনিমেশন টি দেখানো হয়েছে এখানে প্রথমে বামে ঘূর্ণন করা হয়েছে, নোড ৫ কে কেন্দ্র করে এই ঘূর্ণন করা হয়েছে।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | Node *left_right_rotate(Node *node){ Node *temp=node->left_node; //নোড ২ node->left_node=temp->right_node; //২ নং নোড এর জায়গায় ৩ নং নোডকে দিলাম temp->right_node=node->left_node->left_node; //২ নং নোডের ডান সাবট্রি হিসেবে ৩ নং নোডের বাম সাবট্রিকে দিলাম node->left_node->left_node=temp; // ২ নং নোডকে ৩ নং নোডের বাম সাবট্রি হিসেবে সংযুক্ত করলাম //উচ্চতা আপডেট করা হবে এখন int node_2_height=max(height(node->left_node->left_node->left_node),height(node->left_node->left_node->right_node))+1; node->left_node->left_node->height=node_2_height; int node_3_height=max(height(node->left_node->right_node),height(node->left_node->left_node))+1; node->left_node->height=node_3_height; node=right_rotate(node); //নোডকে ডানে ঘুরালাম। return node; } |
উপরে যে লজিক বর্ণনা করেছি, এই কোডটিও একই লজিকে লিখা হয়েছে। আপনরা উপরের এনিমেশনে যেই ট্রি টি দেয়া আছে তাকে খাতায় একে একে বুঝার চেষ্টা করুন। এখানে আমরা বামে ঘূর্ণনের পরে right_rotate(node) কল করেছি, node কে কেন্দ্র করে ডানে ঘুরানোর জন্য।
প্রথমে ডানে তারপর বামে ঘূর্ণন (Right-Left Rotation)

আমাদের গ্রাফে যখন উপরের মতো স্ট্রাকচার তৈরি হবে তখন আমরা Right-Left Rotation করবো।
আমরা যখন প্রথমে নোড ২ এবং নোড ৩ কে ডানে ঘুরাবো তখন, নোড ২, নোড ৩ এর ডান সাবট্রি হবে এবং নোড ৩ নোড ২ এর জায়গা দখল করবে। এবং নোড ৩ এর যদি কোন ডান সাবট্রি থাকে তা নোড ২ এর বাম সাবট্রি হিসেবে সংযুক্ত হবে। এর ব্যাখ্যাও আমাদের Left-Right rotation এর মতোই, পার্থক্য শুধু এটা ডান দিকে ঘটবে এবং নোড ১ এ ।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | Node *right_left_rotate(Node *node){ Node *temp=node->right_node; //নোড ২ node->right_node=temp->left_node; //২ নং নোড এর জায়গায় ৩ নং নোডকে দিলাম temp->left_node=node->right_node->right_node; //২ নং নোডের ডান সাবট্রি হিসেবে ৩ নং নোডের বাম সাবট্রিকে দিলাম node->right_node->right_node=temp; // ২ নং নোডকে ৩ নং নোডের বাম সাবট্রি হিসেবে সংযুক্ত করলাম //উচ্চতা আপডেট করা হবে এখন int node_2_height=max(height(node->right_node->right_node->left_node),height(node->right_node->right_node->right_node))+1; node->right_node->right_node->height=node_2_height; int node_3_height=max(height(node->right_node->right_node),height(node->right_node->left_node))+1; node->right_node->height=node_3_height; node=left_rotate(node); //নোডকে বামে ঘুরালাম। return node; } |
আশা করি আপনারা কোডটি পরেই বুঝবেন। না বুঝলে কমেন্ট করুন। আমি আমার সাধ্যমত চেষ্টা করবো।
উপরে আমরা এতক্ষণ যা যা দেখলাম তা হলো AVL Tree এর জন্য সবথেকে জরুরি বিষয়, AVL Tree height calculation, AVL Tree rotation। আমরা এখন দেখবো কিভাবে কোড ইমপ্লিমেন্ট করা যায়।
AVL Tree insert , C++ এ সম্পূর্ণ ইমপ্লিমেন্টেশন
পূর্বে আমরা AVL Tree insert() ফাংশনের অর্ধেক অংশ (উচ্চতা নির্ণয় পর্যন্ত) দেখেছিলাম। এখন আমরা ঘূর্ণন সহ বাকি অংশ বুঝার চেষ্টা করবো। ঘূর্ণন করতে হলে আমাদের প্রথমে বর্তমান নোডের bf এর মান বের করতে হবে। তার পরে আমাদের দেখতে হবে ট্রি তে কোন ধরনের ভারসাম্যহীনতা তৈরি হয়েছে, তারপর ঐ মোতাবেক ঘূর্ণন করাতে হবে।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | Node *insert(int num,Node *node){ if(node==NULL){ //if node==null হলে আমরা বুঝতে পারবো আমরা বাম, ডান করতে করতে সবার শেষে পৌঁছেছি। রুট নোডের ক্ষেত্রেও এই শর্ত সত্য Node *temp=new Node(); // নতুন একটা নোড তৈরি করি temp->value=num; temp->height=0; return temp; }else if(num<=node->value){ //আমরা বামে যাবো, কারণ আমাদের num এর মান বর্তমান নোডের থেকে কম node->left_node=insert(num,node->left_node); }else{ //আমরা ডানে যাবো, কারণ আমাদের num এর মান বর্তমান নোডের থেকে বেশি node->right_node=insert(num,node->right_node); } //বর্তমান নোড (node) এর ডান এবং বাম সাব-ট্রি এর মধ্যে যার উচ্চতা সব থেকে বেশি, আমাদের বর্তমান নোডের উচ্চতা হবে তার থেকে ১ বেশি। node->height=max(height(node->left_node),height(node->right_node))+1; //সকল রিকার্সিভ হিসাব নিকাশের পরে এখানে আসবে, এখুন আমরা যে সাব-ট্রি তে আছি তার সকল নোডের উচ্চিতা জানি। //তাই আমরা ব্যালেন্স ফ্যাক্টর হিসাব করতে পারবো। int bf=height(node->left_node)-height(node->right_node); //এখন যদি ব্যালেন্স ফ্যাক্টর {-1,0,1} এর বাইরে কিছু হয় তার মানে হলো আনাদের ট্রি/সাবট্রি টি ব্যালেন্স না, তাই আমাদের ব্যালেন্স করে নিতে হবে। if(bf>1){ if(node->left_node->value<num){ // তারমানে Left-Right ভারসাম্যহীনতা node=left_right_rotate(node); }else{ // অথবা Left-Left ভারসাম্যহীনতা node=right_rotate(node); } }else if(bf<-1){ if(node->right_node->value>num){// তারমানে num Right Left ভারসাম্যহীনতা node=right_left_rotate(node); }else{//অথবা Right-Right ভারসাম্যহীনতা node=left_rotate(node); } } return node; } |
এখানে ২০ নং লাইনে আমরা bf (Balance factor) হিসাব করেছি। এই bf এর মান আমাদের বর্তমান নোডের bf কে নির্দেশ করে। যদি bf>1 হয় তাহলে আমরা বলতে পারি আমাদের বাম সাবট্রির উচ্চতা বেশি এবং বাম সাবট্রি ভারসাম্যহীন হয়ে গিয়েছে উপরে ইনসার্ট করার পর। এবং যদি bf<-1 হয় তবে বলতে পারি ডান সাবট্রি ভারসাম্যহীন হয়ে গিয়েছে।
এখন আমাদের চ্যালেঞ্জ হলো কোন ধরনের ঘূর্ণন করা লাগবে তা। এর জন্য আমাদের যা লাগবে তা হলো আমরা মাত্র যেই নোডটি ইনসার্ট করেছি তা কন দিকে গিয়েছে, ডানে নাকি বামে। যদি num এর মান বড় হয় এবং bf এর মান ধনাত্মক হয় () তবে আমরা নিশ্চিত বলতে পারি আমাদের ট্রি তে Left-Right ভারসাম্যহীনতা তৈরি হয়েছে। কারণ AVL Tree কে আমরা কখনো ভারসাম্যহীন রাখবো না। যদি কখন ভারসাম্যহীনতা তৈরি হয় তাহলে এটা সর্বশেষ আপডেট এর জন্যই হয়েছে।

২৪ নং লাইনে পরীক্ষা করা হয়েছে node->left_node->value<num কিনা। যদি এরকম হয় তবে চিত্রের মতো অবস্থা তরি হবে। উপরের অনুচ্ছেদের আলোচনা থেকে বুঝতে পারছি এই শর্ত পূরণ করলেই তবে Left-Right rotation করতে হবে। অন্যথায় Left Left ধরনের ঘূর্ণন করতে হবে।
একই ভাবে আমরা ৩০ নং লাইনে node->right_node->value>num এই শর্ত দিয়ে দেখেছি আমাদের ভারসাম্যহীনতা কি Right-Left ধরনের শর্ত পূরণ করেছে কি না (যেহেতু এক্ষেত্রে )। যদি করে আমরা Right-Left rotation করেছি, নয়তো Right-Right rotation করেছি।
আপনারা হাতে কলমে কোডের ভিজুয়ালাইজ করেন। ইনশাআল্লাহ বুঝতে পারবেন।

চিত্রে Right Left ধরনের ঘূর্ণনের জন্য ট্রি এর ধরন দেখানো হয়েছে। আপনারা শর্তের সাথে মিলিয়ে নিন।
সব শেষে আমরা ৩৬ নং লাইনে node টা কে কলিং ফাংশনের কাছে রিটার্ন করেছি। এভাবেই আমাদের insert function শেষ হয়েছে।
এখন আসি AVL ট্রি তে সার্চ করা নিয়ে। AVL Tree তে সার্চ করার কোড বাইনারি সার্চ ট্রি এর মতোই। কারণ এতে করে ট্রি এর ভারসাম্য নষ্ট হয়ে যাওয়ার ভয় নাই। তাই প্যারা মুক্ত ভাবেই সার্চ করা যাবে। তবে AVL ট্রি তে ডিলেট করার সময় সাবধান থাকতে হবে। কারণ ডিলিট করার সময় ভারসাম্য নষ্ট হতে পারে। তাই ডিলিট এর জন্য আমাদের কোড লিখতে হবে insert এর মতো করে। ওইটা নাহয় আরেকদিন লিখবো। এই লিখা অনেক বেশি বড় হয়ে গিয়েছে। আলাদা আলদা করে পাবলিশ করবো নাকি ভাবছি। কমেন্টে সাজেশন দিয়ে হেল্প করুন। happy_coding;
আরও পড়ার জন্য রিসোর্স AVL Tree Visualization AVL Tree insertion tutorial (Youtube), সোর্স কোড