গ্রাফ থিউরির নতুন একটি লিখায় আপনাদের স্বাগতম। এই লিখায় আমরা মিনিমাম স্পানিং ট্রি (Minimum spanning tree) নিয়ে জানবো এবং ক্রুসকাল অ্যালগরিদমের (Kruskal’s algorithm) মাধ্যমে ইমপ্লিমেন্ট করা দেখবো। ক্রুসকাল অ্যালগরিদম Josheph Kruskal, ১৯৫৬ সালে আবিষ্কার করেন। এই অ্যালগরিদম দিলে আমরা এ মিনিমাম স্প্যানিং ট্রি বের করতে পারি যেখানে হলো গ্রাফের মোট এজ এবং হলো গ্রাফের ভার্টেক্স সংখ্যা।
এই লিখা শুরুর আগে আমরা প্রথমে দেখবো মিনিমাম স্পানিং ট্রি কি? তারপর আমরা ক্রুসকাল অ্যালগরিদম (Kruskal’s algorithm) দেখবো। কিন্তু ক্রুসকাল অ্যালগরিদম নিয়ে দেখার আগে আপনাদের অবশ্যই Disjoint Set Union বা DSU নিয়ে জানতে হবে। (Kruskal’s algorithm Bangla tutorial).
এই অ্যালগরিদমটি প্রথম ১৯৫৬ সালে Proceedings of the American Mathematical Society, pp. 48–50 এ দেখা যায় যেটার লেখক ছিলেম জোসেফ ক্রুসকাল (Joseph Kruskal)।
Prim’s algorithm দিয়েও আমরা মিনিমাম স্প্যানিং ট্রি বের করতে পারি। দেখবো পরের লিখায়।
Minimum spanning tree Bangla tutorial
মিনিমাম স্পানিং ট্রি কি? What is minimum spanning tree?
ধরেন আপনাকে একটি গ্রাফ G দেয়া আছে যেখানে n টা নোড (vertex) এবং m টা এজ (Edge) দেয়া আছে। এখন এখন চলেন আগে জেনে নেই স্পানিং ট্রি কি? (What is a spanning tree?)
স্পানিং ট্রি হল একটি গ্রাফ G এর এমন একটি সাবগ্রাফ যেখানে, n টি নোড n-1 টি এজ দিয়ে কানেক্টেড থাকবে এবং এখানে কোন লুপ থাকবে না। এবার চলেন জেনে নিই মিনিমাম স্পানিং ট্রি কি? মিনিমাম স্পানিং ট্রি হল এমন একটি স্পানিং ট্রি যেখানে এজ গুলোর যোগফল যতদূর সম্ভব সর্বোনিম্ন হয়।
এক কথায় বলতে গেলে একটি গ্রাফের n টি নোড বা Vertex এর সংখ্যা হলে, n সংখ্যক নোড এবং n-1 সংখ্যক এজ (Edge) এমন ভাবে নিয়ে একটি ট্রি তৈরি করতে হবে যেন এজ গুলোর যোগফল যতদূর সম্ভব সর্বনিম্ন হয়। এই ট্রি কে বলা হয় মিনিমাম স্পানিং ট্রি।
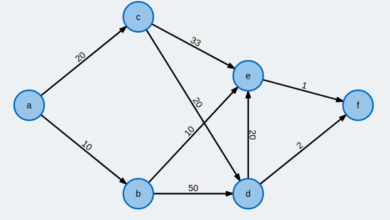
যেহেতু আমাদের ট্রি টি গ্রাফ G থেকে এসেছে। তাই আমরা বলতে পারি যে, মিনিমাম স্পানিং ট্রি টি মূল গ্রাফ এর একটি সাবগ্রাফ যেখানে সর্বোনিম্ন কস্ট (Cost) এ সকল নোড ভিজিট করা যায় ট্রি এর এজ গুলো ব্যবহার করে। নিচের চিত্রটি দেখুন। এখানে একটি weighted গ্রাফ থেকে আমরা একটি মিনিমাম স্পানিং ট্রি বের করেছি।

গ্রাফ G থেকে মিনিমাম স্পানিং ট্রি বের করা- ক্রুসকাল অ্যালগরিদম [Kruskal’s algorithm]
এতক্ষণ আমরা দেখলাম মিনিমাম স্প্যানিং ট্রি কি। এখন আমরা মিনিমাম স্প্যানিং ট্রি বের করার একটি অ্যালগরিদম দেখবো যার নাম ক্রুসকাল অ্যালগরিদম। আবার বলে নেই এই টুকু পরার আগে DSU নিয়ে জানতে হবে। সুতরাং যারা জানেন না তারা আমার এই লিখটি পড়তে পারেন।
Kruskal’s algorithm Bangla tutorial
শুরুতেই আমাদের একটি পয়েন্ট মাথায় রাখতে হবে যে কোন ট্রি তে কখনও লুপ বা সাইকেল থাকবে না। এখন মিনিমাম স্পানিং ট্রি এর শর্তানুসারে আমাদের সব চেয়ে কম খরচে সম্পূর্ণ গ্রাফের সব নোড ভিজিট করতে পারতে হবে।
এই অ্যালগরিদমটি প্রথমেই মোটা দাগে একটু বলে দিই,
- আমাদের যতগুলো এজ (Edge) রয়েছে মূল গ্রাফে সব গুলোকে শুরুতে কস্ট বা weight এর ভিত্তিতে Ascending অর্ডারে সর্ট করে নিবো।
- একটি একটি করে এজ (Edge) লিস্ট থেকে বের করবো এবং যদি দেখি এটা কোন সাইকেল তৈরি করে না তবে এই এজটি আমরা নিয়ে নিবো।
এখন এজ গুলোকে ছোট থেকে বড় বা Ascending অর্ডারে সর্ট করা সহজ। কিন্তু কথা হচ্ছে আমরা কিভাবে চেক করবো যে একটি এজ সাইকেল তৈরি করতেছে কি না?

পাশের/ উপরের (মোবাইলে) চিত্রটি দেখুন। এখানে ডেশ দেয়া এজটিকে (weight 7) আমরা এখনো নিই নি। কিন্তু ৫ ও ৬ weight এর এজ নিয়েছি। এখন ৭ weight এজটি আমরা নিবো কি নিবো না চলুন সিদ্ধান্ত নিই।
এখন নোড ১, নোড ২ এবং নোড ৩, যথাক্রমে ৫ weight এবং 6 weight বিশিষ্ট এজ দারা ইতোমধ্যে যুক্ত বা একই গ্রুপে রয়েছে। এখন আমরা যদি ৭ weight এর এজটি নিই তবে দেখা যাবে এখানে একটি সাইকেল তৈরি হয়ে যাবে। তাই আমরা এই এজটি নিতে পারবো না।
এবার কথা হলো, আমরা কিভাবে চেক করবো কোন দুটি নোড u এবং v একই গ্রুপে আছে কি না। আমরা খেয়াল করে দেখতে পাই যে, নোড ১, ৩ এবং ২ ইতোমধ্যে একই গ্রুপে আছে। এবার আমরা যদি DSU এর মাধ্যমে 2 এবং 3 এর প্যারেন্ট চেক করি তবে দেখতে পারবো এদের প্যারেন্ট একই কিন্তু এই দুটি নোড নিয়েই ৭ weight এর এজটি তৈরি হয়েছে। তাই আমরা এই এজটিকে নিবো না। কারন এই এজটি নিলে ২ এবং ৩ নং নোড যুক্ত হবার কারনে লুপ তৈরি হবে।
সুতরাং আমাদের প্রথমে একটি DSU ইমপ্লেমেন্ট করতে হবে চলুন করে ফেলি।
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | #define n 7 int parent[n]; int find(int x){ //গ্রুপ রিপ্রেজেন্টেটিভ খুঁজে বের করবে। if(parent[x]==x) return x; return parent[x]=find(parent[x]);//path compression } void group(int u,int v){ //ইউনিয়ন অপারেশন করবে। int x=find(u); int y=find(v); if(x!=y){ parent[x]=y; } } |
আশা করি বুঝতে পেরেছেন। আমরা সাধারণ ভাবে একটি DSU ইমপ্লিমেন্ট করেছি। n আমাদের সর্বোচ্চ নোড সংখ্যা নির্দেশ করছে।
এবার চলেন ভবি আমরা গ্রাফের এজ লিস্টকে কিভাবে সর্ট করবো? ধরা যাক আমাদের ইনপুট দেয়া হবে নিচের মত করে।
এখানে m টি নোড ইনপুট দেয়া হবে। u এবং v হলো যথাক্রমে একটি এজ এর শুরুর নোড এবং গন্তব্য নোড। w হলো এজটির weight। যেখানে । এবার এইগুলো ইনপুট নেয়ার জন্য আমরা একটি স্ট্রাকচার তৈরি করবো যেখানে u, v এবং w এর মান জমা রাখবো।
| 1 2 3 4 5 6 7 8 | struct Edge{ Edge(int u,int v,int w){ this->u=u; this->v=v; this->w=w; } int u,v,w; }; |
এবার আমরা একটি অ্যারে edges[m] নিবো যেটি হবে Edge ডাটা টাইপের এবং সাইজ m৷
| 1 2 3 | int m; cin>>m; //input the number of edges Edge edges[m]; |
এখানে m হলো আমরা কয়টি এজ ইনপুট দিবো তার সংখ্যা। আমরা m ইনপুট নিয়েছি এবং পরে m সাইজের একটি অ্যারে নিয়েছি এজগুলোকে রাখার জন্য। এবার চলেন এজ গুলোকে ইনপুট নেয়া যাক।
| 1 2 3 4 | for(int i=0;i<m;i++){ int u,v,w; cin>>edges[i].u>>edges[i].v>>edges[i].w; } |
এখন আমরা আমাদের অ্যারেকে সর্ট করে নিবো। এক্ষেত্রে অমি STL sort() ফাংশন ব্যবহার করবো এবং কম্পেয়ার করার জন্য একটি কম্পেয়ার ফাংশন cmp(Edge x, Edge y) ব্যবহার করবো।
| 1 2 3 4 5 6 | //@এইটুকু মেইন এর উপরে যাবে bool cmp(Edge x,Edge y){ return x.w<y.w; } // এইটুকু ইনপুট নেয়ার পরে। sort(edges,edges+m,cmp); |
এবার আমরা প্রস্তুত। আমরা নিচের মত করে কাজ করবো। Edge অ্যারের 0 থেকে পর্যন্ত যতগুলো এজ আছে প্রত্যেককে একে একে করে নিবো এবং একটি ভ্যারিয়েবল e তে রাখবো। তারপর যদি find(e.u)!=find(e.v) হয় তারমানে দুইটি নোড আলাদা গ্রুপে রয়েছে, তাই এই এজটি কোন সাইকেল তৈরি করবে না। আমরা এজটি নিয়ে নিবো আর e.u এবং e.v কে একই গ্রুপে পরিণত করবো group(e.u,e.v) কল করার মাধ্যমে। আমরা চাইলে এই এজের weight যোগ করে রেখে মিনিমাম কস্ট প্রিন্ট করতে পারবো। চলুন ইমপ্লিমেন্ট করি।
| 1 2 3 4 5 6 7 8 9 10 | int minCost=0; for(int i=0;i<m;i++){ Edge e=edges[i]; if(find(e.u)!=find(e.v)){ group(e.u,e.v); minCost+=e.w; cout<<e.u<<" থেকে "<<e.v<<" পর্যন্ত এজটি নেয়া হলো।\n"; } } cout<<"সর্বোনিম্ন খরচ হবে: "<<minCost<<endl; |
নিচের অ্যানিমেশনটি দেখুন
আশা করি বুঝেছেন কি করেছি। নিচে অমি সম্পূর্ণ কোডটি দিয়ে রাখলাম।
Kruskal’s algorithm Bangla: full code C++ implementation
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | #include <bits/stdc++.h> using namespace std; #define n 7 int parent[n]; int find(int x){ if(parent[x]==x) return x; return parent[x]=find(parent[x]);//path compression } void group(int u,int v){ int x=find(u); int y=find(v); if(x!=y){ parent[x]=y; } } struct Edge{ int u,v,w; }; bool cmp(Edge x,Edge y){ return x.w<y.w; } int main(){ for(int i=0;i<n;i++) parent[i]=i; int m; cin>>m; //input the number of edges Edge edges[m]; for(int i=0;i<m;i++){ int u,v,w; cin>>edges[i].u>>edges[i].v>>edges[i].w; } sort(edges,edges+m,cmp); int minCost=0; for(int i=0;i<m;i++){ Edge e=edges[i]; if(find(e.u)!=find(e.v)){ group(e.u,e.v); minCost+=e.w; cout<<e.u<<" থেকে "<<e.v<<" পর্যন্ত এজটি নেয়া হলো।\n"; } } cout<<"সর্বোনিম্ন খরচ হবে: "<<minCost<<endl; } |
সবার প্রথমে দেয়া চিত্রের মত আউটপুট পেতে নিচের মত ইনপুট দিন। (Kruskal’s algorithm Bangla)
| ইনপুট | আউটপুট |
| 8 1 2 5 1 3 2 2 3 9 2 4 3 3 4 2 4 5 3 4 6 1 5 6 8 | 4 থেকে 6 পর্যন্ত এজটি নেয়া হলো। 1 থেকে 3 পর্যন্ত এজটি নেয়া হলো। 3 থেকে 4 পর্যন্ত এজটি নেয়া হলো। 2 থেকে 4 পর্যন্ত এজটি নেয়া হলো। 4 থেকে 5 পর্যন্ত এজটি নেয়া হলো। সর্বোনিম্ন খরচ হবে: 11 |
Practice Problems (CP Algorithm)
- Codeforces – Edges in MST
- Codeforces – Flea
- Codeforces – Igon in Museum
- Codeforces – Hongcow Builds a Nation
আজকের লিখা এই পর্যন্তই থাকল. লিখাটি রেট করতে ভুলবেন না। পরবর্তীতে হাজির হব অন্য একটি লিখায়। সেই পর্যন্ত #happy_coding.