ডিসজয়েন্ট সেট ইউনিয়ন (Disjoint Set Union/ DSU) যাকে প্রধান দুটি অপারেশন এর নাম অনুসারে ইউনিয়ন ফাইন্ড (Union-Find) হিসেবেও জানি তার মাধ্যমে কিছু নোড একই সেটে আছে কি না তা বের করতে পারি। ধরা যাক আপনার কাছে A, B, C, D, E নামে পাঁচটি ইলিমেন্ট আছে। তো আমরা বলে দিলাম A, B এর একই সেটে আছে এবং B, C এর একই সেটে আছে। তাই আমরা বলতে পারি A, C এর ও একই সেটে আছে। এখন আবার বলে দিলাম D, E এর একই সেটের। তারপর আপনাকে প্রশ্ন করলাম B কি E কি একই সেটের সদস্য? উত্তর হবে না। আবার যদি একই প্রশ্ন করি E, Dক্ষেত্রে? উত্তর হবে হ্যাঁ।নিচে এই বিষয়টাকে গ্রাফের মাধ্যমে দেখার চেষ্টা করি।
Disjoint Set Union (DSU)/ Union Find Bangla tutorial

এখানে A, B, C একই সেটের সদস্য। A, C সরাসরি কানেক্টেড না হলেও একই গ্রুপের হবার জন্য বন্ধু হিসেবে গণ্য হবে।
আবার D, E একই সেটের সদস্য। কিন্তু এই সেটের সাথে সবুজ সেটের সম্পর্ক না থাকায় B, E একই সেটের সদস্য হবে না।
এখন আমাদের সমস্যা হলো আমাদের কিছু ডেটাকে সেটভুক্ত করতে হবে (Union) এবং পরে বের করতে হবে একটি ডেটা কোন সেটে আছে (Find)।
ডিসজয়েন্ট সেট ইউনিয়ন (Disjoint Set Union) বা DSU এর দুইটি প্রধান অপারেশন রয়েছে। যথা,
(১) Union: দুটি ডেটা কে একই সেটের অন্তর্ভুক্ত করা।
(২) Find: একটি ডেটা কোন সেটে আছে তা খুঁজে বের করা।
প্রথমেই আমাদের যা করতে হবে তা হলো, প্রতিটি সেটের জন্য একটি নোডকে রিপ্রেজেন্টেটিভ করা। রিপ্রেজেন্টেটিভ এর আইডিয়াটি অনেকটা ক্রিকেট খেলার ক্যাপ্টেনের মতো। যেমন বাংলাদেশ দলের ক্যাপ্টেন সম্পূর্ণ বাংলাদেশ দলের প্রতিনিধি বা রিপ্রেজেন্টেটিভ, একই ভাবে জিম্বাবুয়ে দলের ক্যাপ্টেন তাদের দলের সব খেলোয়াড়ের রিপ্রেজেন্টেটিভ।
এখন এই দুই দলের কোন একজন খেলোয়াড়কে যদি প্রশ্ন করি আপনার ক্যাপ্টেন কে, ক্যাপ্টেনের নাম জানার পর আমরা বুঝে যাবো উনি কোন দলের খেলোয়াড়। একই ভাবে দুইজন খেলোয়াড়ের ক্যাপ্টেনের নাম যদি একই হয় তবে বলতে পারবো দুইজন খেলোয়াড় একই দলের।
ধরা যাক আমরা 1 থেকে 10 পর্যন্ত ডেটা গুলোকে সেট করবো, এই প্রতিটি সংখ্যা একেকটি নোড। এর জন্য দুইটি ফাংশন ডিফাইন করলাম। একটি হলো void union_set(int a,int b); যেটি a সহ a এর সম্পূর্ণ সেট এবং b সহ b এর সম্পূর্ণ সেট কে মার্জ করবে। অন্য ফাংশনটি হলো int find(int a); যেই ফাংশনটি a এর রিপ্রেসেন্টেটিভ কে খুঁজে বের করবে।
ডিসজয়েন্ট সেট ইউনিয়ন পুরোপুরি বুঝার জন্য নিচের চিত্রগুলো দেখি,
ধরা যাক আমাদেরকে ১ থেকে ১০ পর্যন্ত সংখাগুলো নিয়ে কিছু সেট অপারেশন করা লাগবে। আমরা union_set(a,b); এর মাধ্যমে কে একই সেট ভুক্ত করবো এবং find(a); এর মাধ্যমে এর রিপ্রেজেন্টেটিভ খুঁজে বের করবো।

অপারেশন করার আগে আমরা একটি অ্যারে নিবো 11 সাইজের (0 থেকে 10 পর্যন্ত ইনডেক্স থাকবে তাহলে)। যেহেতু অপারেশনের শুরুতে কোন সেটকে ইউনিয়ন করা হয়নি, তাই আমরা প্রত্যেককে প্রত্যেকের রিপ্রেজেন্টেটিভ হিসেবে ধরে নিবো। অর্থাৎ এর রিপ্রেজেন্টেন্টিভ হবে নিজেই।
union_set(a,b) ফাংশনটি b এর রিপ্রেজেন্টেটিভ এর প্যারেন্ট হিসেবে a এর রিপ্রেজেন্টেটিভ কে এসাইন করা দিবে।
এখন ধরা যাক আমরা union_set(1,2); করবো। তাহলে আমরা যা করবো 2 এর রিপ্রেজেন্টেটিভ হিসেবে 1 কে সেট করে দিবো যেহেতু 1 এর রিপ্রেজেন্টেন্টিভ 1 নিজেই, এবং 2 এর রিপ্রেজেন্টেন্টিভ 2 নিজেই।। আবার ধরা যাক union_set(4,7); করবো। তখন একইভাবে 7 এর রিপ্রেজেন্টেটিভ হিসেবে 4 কে সেট করে দিবো,

এখন ধরা যাক আমরা union_set(2,7); করতে চাই (কমলা গ্রুপ এবং সবুজ গ্রুপ একসাথে করতে হবে)। উপরের চিত্রে লক্ষ করি, 7 এর রিপ্রেজেন্টেটিভ 4, অপরদিকে 2 এর রিপ্রেজেন্টেটিভ 1। তাই যদি আমরা 1 কে 4 এর রিপ্রেজেন্টেটিভ করে দিই, তাহলে কিন্তু বলতে পারবো 7 এবং 2 একই সেটের সদস্য।

লক্ষ করি 7 এবং 2 একই সেটের সদস্য হলেও (রিপ্রেজেন্টেটিভ একই) 7 এবং 2 এর প্যারেন্ট কিন্তু একই নয়, 7 এর প্যারেন্ট 4 এবং 2 এর প্যারেন্ট 1। এতক্ষণে হয়তো এর অ্যালগরিদম কেমন হবে, অনেকে মাথায় ধারনা এসে গেছে। চলুন অ্যালগরিদমটি দেখে আসি।
আমরা ধরে নিই, a এবং b কে ইউনিয়ন করবো। তাহলে
- x=a এর রিপ্রেজেন্টেটিভ খুঁজে বের করি।
- y=b এর রিপ্রেজেন্টেটিভ খুঁজে বের করি।
- যদি a এর রিপ্রেজেন্টেটিভ এবং b এর রিপ্রেজেন্টেটিভ সমান না হয় ( x!=y) , তবে x কে y এর প্যারেন্ট করে দিই।
এটুকুই। এখন x এবং y যদি সমান হয় তবে আমরা বলতে পারি a, b অবশ্যই একই সেটের সদস্য। তখন আমাদের কিছু করার দরকার নেই।
উপরের অ্যালগরিদম অনুসারে আমরা নিচের মত অপারেশন করা শেষ হলে আমাদের সবার শেষে সেট টি দেখতে এমন হবে।
- union_set(1,2);
- union_set(4,7);
- union_set(2,7);
- union_set(7,9);
- union_set(7,6);
- union_set(9,10);
- union_set(10,3);
- union_set(3,5);
- union_set(7,3);
- union_set(1,8);
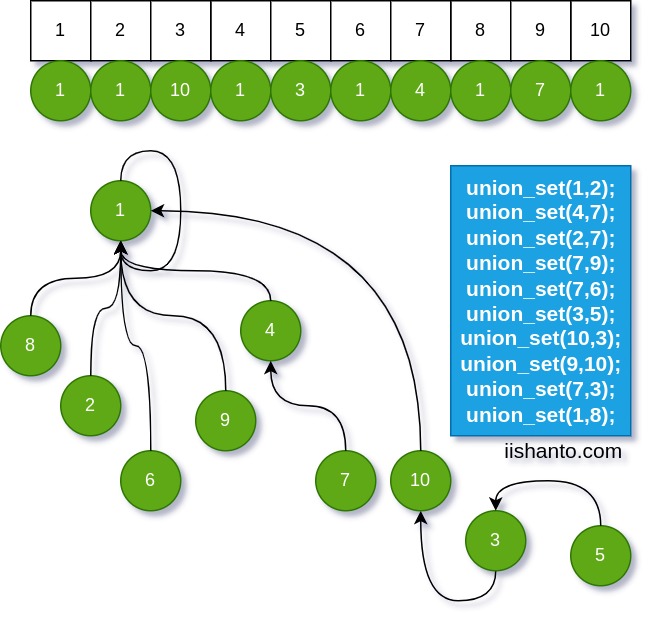
সবথেকে ভালো হয় যদি খাতা কলমে আপনি অপারেশন গুলো ভিজুয়ালাইজ করতে পারেন।
রিপেজেন্টেটিভ খুঁজার জন্য find() ফাংশন এর অ্যালগরিদম।
ধরা যাক আমরা find(5); বা 5 এর রিপ্রেজেন্টেটিভ খুঁজতে চাই। তাহলে, আমরা প্রথমে 5 এর প্যারেন্ট বা 3 এর কে খুঁজে বের করবো। তারপর 3 এর প্যারেন্ট 10 এর কাছে যাবো, তারপর 10 এর প্যারেন্ট 1 এর কাছে যাবো। এখন যেহেতু 1 এর প্যারেন্ট 1 নিজেই, তাই এই সেটের রিপ্রেজেন্টেটিভ 1। অতএব আমরা রিকার্শন এর মাধ্যমে চাইল্ড থেকে প্যারেন্টে যেতে থাকবো যতক্ষণ না এমন নোডে যাই যেখানে নোড আর প্যারেন্ট একই হয়। তারপর রিটার্ন করে দিবো।
| 1 2 3 4 5 6 | int find(int a){ // a এর রিপ্রেজেন্টেটিভ খুঁজতে হবে। if(a==parent[a]){ // যখন a==parent[a] হবে তার মানে আমরা রিপ্রেজেন্টেটিভে চলে এসেছি। return a; } return find(parent[a]); // অথবা a এর প্যারেন্ট যে তার রিপ্রেজেন্টেটিভ খুঁজতে হবে। } |
উপরের উদাহরণে find(5); খুঁজতে গেলে এভাবে ফাংশন কল হবে,
প্রথমে find(5) কল করা হবে, তারপর 5 এর প্যারেন্ট বা find(3) কল করা হবে। এখন 3 এর প্যারেন্ট 10 তাই find(10) কল হবে। এখন 10 এর প্যারেন্ট সে নিজেই। তাই a==parent[a] এটা সত্য হবে এবং 1 রিটার্ন হবে।
উপরের কোডের কমপ্লেক্সিটি O(n)। আমরা খুব সহজেই এই কোডকে দ্রুতগতির করতে পারি। আমরা একটু পরেই দেখবো।
ডিসজয়েন্ট সেট ইউনিয়ন: union_set() ফাংশনে ইমপ্লিমেন্টেশন
উপরে union করার অ্যালগরিদম দেখে এসেছি। আমরা এখন তাই ইমপ্লিমেন্ট করবো। চলুন কোডটি দেখি।
| 1 2 3 4 5 6 7 | void union_set(int a,int b){ int x=find(a); //a এর রিপ্রেজেন্টেটিভ খুঁজে বের করি। int y=find(b); //b এর রিপ্রেজেন্টেটিভ খুঁজে বের করি। if(x!=y){// যদি x,y একই সেটের সদস্য না হয় তবে parent[y]=x; //y এর প্যারেন্ট হিসেবে x কে সেট করে দিলাম। } } |
এই কোড । এখন এই কোডের কমপ্লেক্সিটি কত? উপরে find() ফাংশনের কমপ্লেক্সিটি O(n)। আমরা চাইলে একে Path compression এর মাধ্যমে প্রায় করতে পারি।
পাথ কমপ্রেশন- Path compression algorithm Bangla tutorial
find(7) ফাংশন কি করছে? 5->3->10->1 হয়ে রিপ্রেজেন্টেটিভ খুঁজে দিচ্ছে। এখন এমরা যদি কোনোভাবে 5->3->10->1 কে এমন ভাবে কমপ্রেস করতে পারি যেন 5 থেকে সরাসরি 1 এ যাওয়া যায় তবে কিন্তু আমাদের কাজ অনেক দ্রুত হয়ে যাবে। এর জন্য আমরা শুধু একটু পরিবর্তন করবো find() এর রিটার্ন স্টেটমেন্টে।
| 1 2 3 4 5 6 7 | int find(int a){ // a এর রিপ্রেজেন্টেটিভ খুঁজতে হবে। if(a==parent[a]){ // যখন a==parent[a] হবে তার মানে আমরা রিপ্রেজেন্টেটিভে চলে এসেছি। return a; } parent[a]=find(parent[a]); // অথবা a এর প্যারেন্ট যে তার রিপ্রেজেন্টেটিভ খুঁজতে হবে। return parent[a]; } |
উপরের কোডে লক্ষ করি, parent[a]=find(parent[a]);এর মাধ্যমে আমরা a এর প্যারেন্ট হিসেবে রিপ্রেজেন্টেটিভকে দিয়ে দিয়েছি। এখানে find(parent[a]); এ সবসময় ই সেটের রিপ্রেজেন্টেটিভ কে রিটার্ন করবে। রিটার্ন করার পর যখন আমরা parent[a] বা a এর প্যারেন্ট হিসেবে সেই রিপ্রেজেন্টেটিভকে সেট করে দিলাম। এতে করে আমরা সরাসরি রিপ্রেজেন্টেটিভ কে পাবো, এবং বাড়তি রিকার্শন স্কিপ করতে পারবো।
এর উদাহরণ হিসেবে আমরা ধরি উপরের ট্রিতে find(5) কল করলাম, তারপর নিচের মত করে ট্রি টি কমপ্রেস হয়ে যাবে।

আশা করি বুঝা গেছে, আমরা যতবার find(a) কল করবো তা union_set() ফাংশনের ভেতরে বা বাইরে যেখানেই হোক, ততবার আমাদের এভাবে আপডেট হতে থাকবে।
এবার আমরা সম্পূর্ণ কোডটি দেখবো, পুরো কোডটি C++ এ করা।
DSU/ Disjoint Set Union Data structure implementation using C++
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | /* Sharif Hasan - CSE, PUST */ #include<bits/stdc++.h> using namespace std; int parent[11]; int find(int a){ // a এর রিপ্রেজেন্টেটিভ খুঁজতে হবে। if(a==parent[a]){ // যখন a==parent[a] হবে তার মানে আমরা রিপ্রেজেন্টেটিভে চলে এসেছি। return a; } parent[a]=find(parent[a]); return parent[a]; // অথবা a এর প্যারেন্ট যে তার রিপ্রেজেন্টেটিভ খুঁজতে হবে। } void union_set(int a,int b){ int x=find(a); //a এর রিপ্রেজেন্টেটিভ খুঁজে বের করি। int y=find(b); //b এর রিপ্রেজেন্টেটিভ খুঁজে বের করি। if(x!=y){// যদি x,y একই সেটের সদস্য না হয় তবে parent[y]=x; //y এর প্যারেন্ট হিসেবে x কে সেট করে দিলাম। } } int main(){ for(int i=0;i<11;i++){ parent[i]=i; //i এর রিপ্রেজেন্টেটিভ হিসেবে প্রথমে i কেই সেট করে দিলাম } // একটি সেট তৈরি করলাম union_set(1,2); union_set(1,3); union_set(3,10); //অপর আরেকটি সেট তৈরি করলাম union_set(4,5); union_set(5,8); union_set(7,6); union_set(6,8); int a,b; cin>>a>>b; if(find(a)==find(b)){ // a,b একই সেটের হলে রিপ্রেজেন্টেটিভ একই হবে cout<<a<<" and "<<b<<" are in same set!\n"; }else{ cout<<a<<" and "<<b<<" are in different set!\n"; } } |
এখানে যদি আমরা লক্ষ করি, union_set() তার মূল কাজ করেছে সময়ে। আমাদের টাইম কমপ্লেক্সিটি মূলত find() ফাংশনের কমপ্লেক্সিটির উপর নির্ভর করছে। n টি নোডের উপর আমরা যদি পাথ কমপ্রেশনের মাধ্যমে m টি অপারেশন করি, তবে আমাদের সর্বমোট কমপ্লেক্সিটি হবে ।
আজকে এই পর্যন্তই। ডিসজয়েন্ট সেট ইউনিয়ন ডাটা স্ট্রাকচারটির অনেক অ্যাপ্লিকেশন রয়েছে। পরবর্তীতে গ্রাফ থেকে মিনিমাম স্পানিং ট্রি বের করার জন্য যখন Kruskal’s algorithm দেখবো তখন এই ডাটা স্ট্রাকচারটি লাগবে। আজ এই পর্যন্তই। #happy_coding.
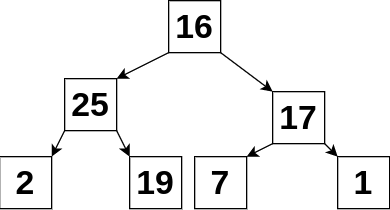
এক কথায় “অসাধারণ”
Thank you brother <3