বাইনারি এক্সপোনেন্টিয়েশন অ্যালগরিদম ব্যবহার করে আরেকটি লিখা আছে আমার ব্লগে, সংখ্যাতত্ত্ব: মডুলার অ্যারিথমেটিক (Modular arithmetic) – Big mod, এই লিখাতেও আমি রিকার্শনের মাধ্যমে কিভাবে অ্যালগরিদমের ইমপ্লিমেন্ট করতে হয় তা ব্যাখ্যা করেছি। এই লিখাটিতে আমরা মূলত এটাই দেখবো, তবে বিগ মোড বাদ দিয়ে এবং ইটারেটিভ পদ্ধতিতে। এই লেখাতে দেখবো কিভাবে বাইনারি পদ্ধতিতে এর মান বের করা যায়।
Binary Exponentiation Bangla Tutorial
সাধারণভাবে এর মান যখন বের করি তখন কি করি? n সংখ্যক a কে 1 এর সাথে গুন করি। কিন্তু এই পদ্ধতির টাইম কমপ্লেক্সিটি , আমরা একে চাইলেই এর নামিয়ে ফেলতে পারি বাইনারি এক্সপোনেন্টিয়েশন পদ্ধতি কাজে লাগিয়ে।
বাইনারি এক্সপোনেন্টিয়েশন কে অনেক সময় বর্গের মাধ্যমে এক্সপোনেন্টিয়েশন বা সূচকের মান বের করাও বলা হয়। এর মাধ্যমে আমরা O(log n) এ সূচকের মান বের করতে পারি।
শুরুতেই আমরা একটি হাইস্কুলের অংক দেখে নেই। যদি হয় তবে হবে। সূচকের সূত্র প্রয়োগ করে পাই, । ঠিক এই আইডিয়াটিই এখন প্রয়োগ করবো। জানা আছে যেকোনো সংখ্যাকে কতগুলো ২ এর সূচকীয় মানের যোগফল আকারে প্রকাশ করা যায়।
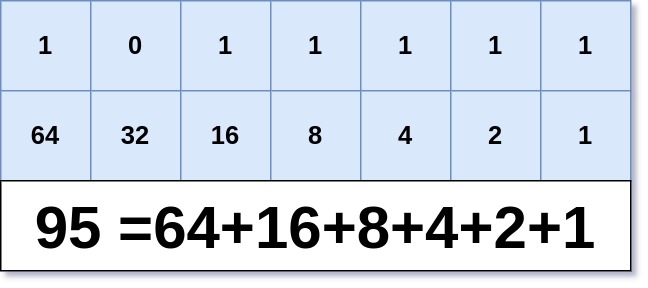
উদাহরণ হিসেবে 95 কে নেই। এর বাইনারি মান বের করে পাই, । আমরা যদি ডান থেকে বামে শুন্য থেকে শুরু করি, তবে সর্বডানের ইনডেক্স 0 এবং সর্ব বামের ইনডেক্স 6। খেয়াল করি, যেখানে যেখানে 1 আছে, তাদের ইনডেক্স ডান থেকে বামে যথাক্রমে, , ইনডেক্স 5 বাদ গিয়েছে কারণ এর বিট 0। এই জায়গা গুলোর সূচকীয় মান বের করবো সূত্র ব্যবহার করে, তাই ।
একইভাবে 13 কে আমরা লিখতে পারি, । আমরা যদি বের করতে চাই, যেখানে তবে,
বা এখন আমরা খুব সহজেই এবং এর মান বের করে ফেলতে পারবো। প্রথমে বের করবো, তারপর বের করবো। তারপর এর মান বেরিয়ে যাবে। এর পরে এর মানও বেরিয়ে যাবে। দেখতে পাচ্ছি, আমরা খুব সহজেই এর মান বের করতে পারি। সুতরাং বলা যায় আমরা ডান থেকে বামে আসার সময় পর্যায়ক্রমিক ভাবে বর্গ করলেই সূচকীয় মান গুলি O(1) এই বের করতে পারবো।
আমি ধরে নিচ্ছি আপনারা দশমিক থেকে বাইনারিতে রূপান্তরের অ্যালগরিদম জানেন। আমরা এখন লুপের মাধ্যমে উপরে যা কিছু বলেছি তার ইমপ্লিমেন্ট করবো। যারা করেন নি তারা আগে দশমিক থেকে বাইনারি রূপান্তরের কোডটি দেখে নিলে ভালো হয়।
| 1 2 3 4 5 6 7 8 9 10 11 12 | long long bin_pow(long long a,long long n){ long long ans=1,current=a; while(n>0){ int r=n%2; n/=2; if(r==1){ // যেই বিট গুলো সেট করা শুধু তারাই বিবেচ্য ans*=current; } current=current*current; } return ans; } |
এই লুপের অপারেশন করতে সময় লাগবে। কারণ কোনও সংখ্যাকে সর্বোচ্চ সংখ্যক বাইনারি ডিজিট দিয়ে প্রকাশ করা যায়।
এই কোডে আমরা বের করার জন্য a, n কে প্যারামিটারের মাধ্যমে ইনপুট নিয়েছি। r ভারিয়েবলে তাদের n%2 বা n কে ২ দ্বারা ভাগ করার পর ভাগশেষ জমা রেখেছি এবং তারপর একে দুই দ্বারা ভাগ করার পর ভাগফল n এ জমা রেখেছি পরবর্তী হিসেব এর জন্য।
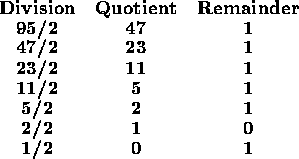
উপরের চিত্রটি আমাদের কোডের লুপটিকে ব্যাখ্যা করছে। শুরুতে n=95, একে 2 দ্বারা ভাগ করার পর Quotient বা n কে ৪৭ দ্বারা আপডেট করা হয়েছে, এবং ভাগশেষ 1 হিসেবে r বা remainder ভেরিয়েবল এ জমা রাখা হয়েছে। তারপরের লাইন গুলোতেও n এর উপর একই ধরনের কাজ পুনরাবৃত্তি করা হয়েছে। এখন আমরা জানি এক্ষেত্রে শেষের বিটটি MSB (Most Significant Bit) এবং প্রথমটি LSB (Least Significant Bit)। তাই আমরা শেষ থেকে শুরুর দিকে বিট গুলো লিখে পাই, ।
কোডের ৭ নং লাইনে কোন বিট হলে তার মানকে আমরা উপেক্ষা করেছি যার জন্য ৩২ কে আমরা বাদ দিয়ে দিয়েছি। কিন্তু যেহেতু এ আমাদের প্রতিটি সূচকের মান লাগবে (উদাহরণ সরূপ বের করতে হলে জানতে হয়) তাই কোডের ৯ নং লাইনে আবার গেলে দেখতে পারবো current = current*current, অর্থাৎ আমরা প্রতিটি বিটের জন্যই যেখানে x হলো ২ এর যেকোনো সূচকীয় মান, তা বের করে নিয়েছি। তারপর যেই বিট গুলো 1 আছে ওসব ক্ষেত্রে আমরা ans এর সাথে গুন করে দিয়েছি।
রিকার্শনের মাধ্যমে বাইনারি এক্সপোনেন্টিয়েশন
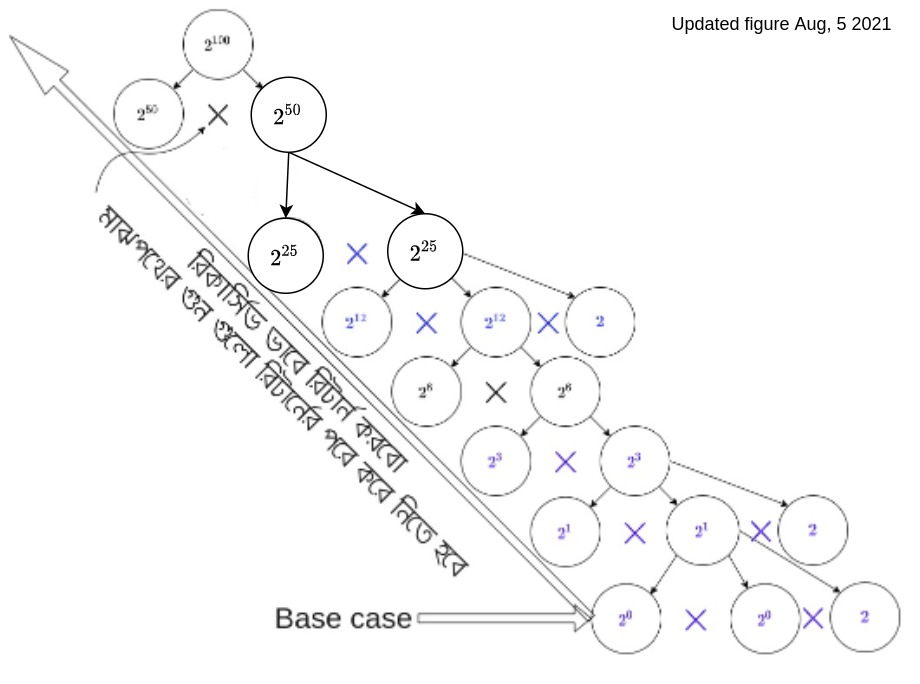
ধরা যাক আমাদেরকে বের করতে বলা হয়েছে। আমরা প্রথম পদ্ধতি বাদেও খুব সহজে রিকার্শনের মাধ্যমে এটা ইমপ্লিমেন্ট করতে পারি। উপরের চিত্রটি দেখি। error যার জন্য আমরা রিকার্সিভ কলের মাধ্যমে আগে বের করেছি। বের করতে গিয়ে আমরা রিকার্সিভ কলের মাধ্যমে বের করেছি কারণ । এখন এর সূচক 25 একটি বিজোড় সংখ্যা। তাই আমরা রিকার্সিভ কলের মাধ্যমে বের করেছি এবং এর সাথে 2 গুন করে দিয়েছি। এভাবে আমরা সূচককে প্রতিবারে দুইভাগ করেছি এবং রিকার্সিভ ভাবে অর্ধেক সূচকের জন্য মান বের করেছি। এভাবে আমরা বেস কেস যেখানে সূচক 0 সেখানে পৌঁছেছি। কোডটি দেখলেই আশা করি বুঝা যাবে।
| 1 2 3 4 5 6 7 8 | int big_mod(int a,int n){ cout<<"Finding "<<a<<"^"<<n<<endl; if(n==0) return 1; int x=big_mod(a,n/2); x= x*x; if(n%2==1) x=x*a; // যদি সূচক বিজোড় হয় return x; } |
উপরের চিত্রের প্রসেসটাই এই ফাংশনে ইমপ্লিমেন্ট করা হয়েছে।
প্রাকটিস প্রবলেম http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=24&page=show_problem&problem=3671
আজকের লিখা এই পর্যন্তই। পরের লিখায় ইউক্লিডীয় অ্যালগরিদম এবং বর্ধিত ইউক্লিডীয় অ্যালগরিদম নিয়ে আসবো। সেই পর্যন্ত #happy_coding.



